持续整理中
【时间序列预测】Are Transformers Effective for Time Series Forecasting?
香港中文大学曾爱玲文章,在长时间序列预测问题上使用线性模型打败基于 Transformer 的模型,并对已有模型的能力进行实验分析(灵魂7问,强烈推荐好好读一下!)。
滴滴和华南理工在 2022 年 KDD 上发表的 ETA 论文,从多个视角解释轨迹,引入 Hierarchical Self-Attention Network 方法进行建模,最终在滴滴内部数据集上获得指标提升。
【Uber ETA】DeeprETA An ETA Post-processing System at Scale
本篇文章充满工业界风格,介绍 Uber 如何构建基于深度学习的 ETA 系统。在 Uber App 中,ETA 主要服务网约车和外卖两大业务,基于业务发展产生出一些细分场景的 ETA 需求(pick-up、drop-off)。技术挑战在于偏航(系统预估路线和司机真实路线不同)、不同场景数据分布不同、不同场景对 ETA 诉求不同,所以他们主要目标是构建高效以及泛用的 ETA 系统。
国庆节前突然对如何计算 BERT 的参数量感兴趣,不过一直看不明白网上的计算过程,索性下载 BERT 源代码阅读一番。这篇文章记录阅读 BertModel 类(核心代码实现)时写的一些笔记,反正我也是纸上谈兵,所以不需要太关注数据处理和 Finetune 相关部分,最后附上计算 BERT 参数量的过程仅供参考。
李宏毅强化学习课程笔记 Imitation Learning
我的笔记汇总:
- Policy Gradient、PPO: Proximal Policy Optimization、Q-Learning
- Actor Critic
- Sparse Reward
- Imitation Learning
apprenticeship learning
- 无法从环境中获得 reward。
- 某些任务中很难定义 reward。
- 人为设计的奖励可能导致意外的行为。
学习专家的行为。
Behavior Cloning
监督学习,但是样本有限。
Dataset Aggregation
- 通过行为克隆得到 actor
- 利用 和环境交互得到一些新的样本
- 由专家对上一步采样得到的样本进行标注
- 利用新得到的样本训练
如果机器的学习能力有限,可能复制专家多余无用的动作。监督学习无法区分哪些是需要学习、哪些是需要忽视的行为。
Miss match
监督学习中,我们假设训练数据和测试数据有相同的分布。Behavior Cloning 中可能分布不同。

Inverse Reinfofcement Learning
反向强化学习
没有 reward 函数,通过专家和环境互动学到一个 reward function,然后再训练 actor。
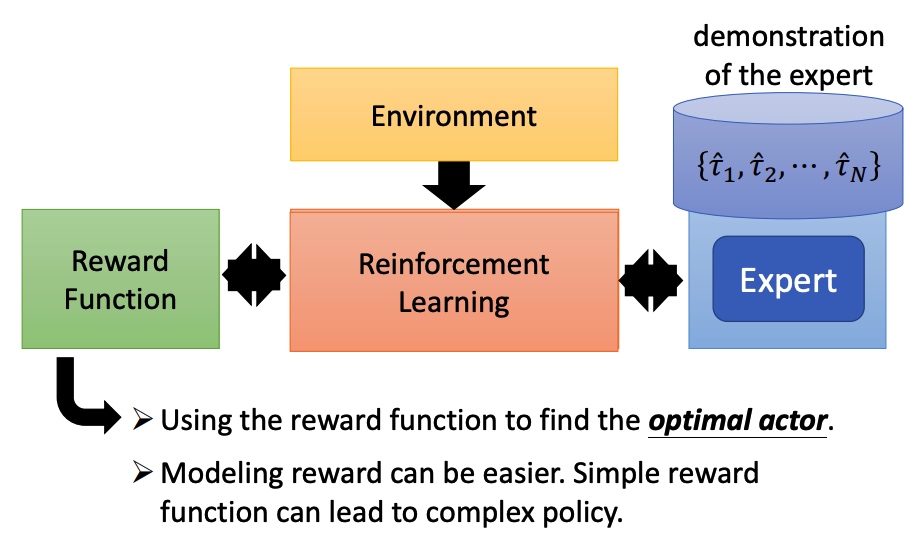
类似于 GAN 的训练方法(actor 换成 generator,reward function 换成 discriminator)。
学到 actor 的 pi 后,调整 reward function,保证专家的行为得分大于学到的行为。
我的笔记汇总:
- Policy Gradient、PPO: Proximal Policy Optimization、Q-Learning
- Actor Critic
- Sparse Reward
- Imitation Learning
Reward Shaping
如果 reward 分布非常稀疏的时候,actor 会很难学习,所以刻意设计 reward 引导模型学习。
Curiosity Intrinsic Curiosity module (ICM)
在原来 Reward 函数的基础上,引入 ICM 函数。ICM 鼓励模型去探索新的动作。最后 ICM 和 Reward 和越大越好。
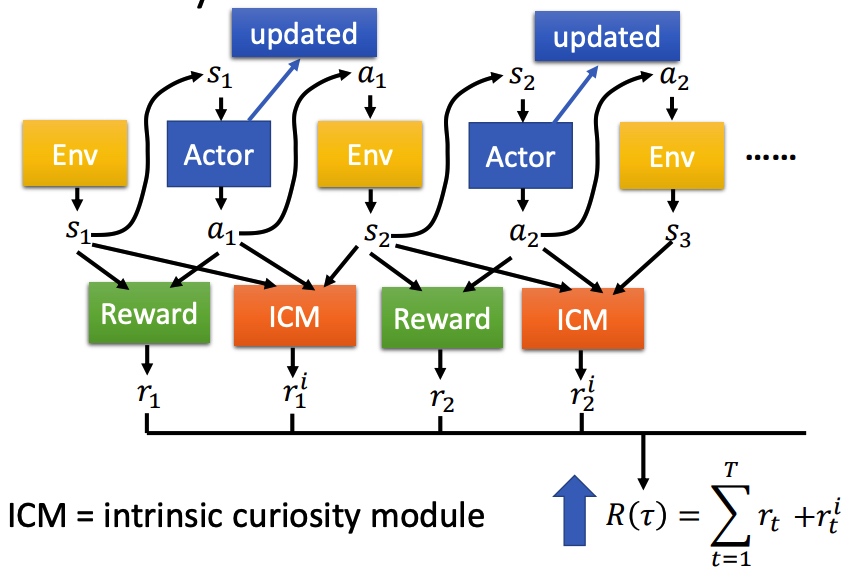
鼓励探索新动作之后,会导致系统风险变大。对比预测的下一个状态和真正的状态的差异程度进行抑制。

Feature Ext 对状态进行抽取,过滤没有意义的内容。
Network 1 预测下一个状态,然后再和真实状态计算 diff 程度。
Network 2 预测 action,和真实的 action 进行对比。如果两个 action 接近,说明 f 可以进行特征提取。重要程度计算。
Curriculum Learning
规划学习路线,从简单任务学习。
Reverse Curriculum Generation
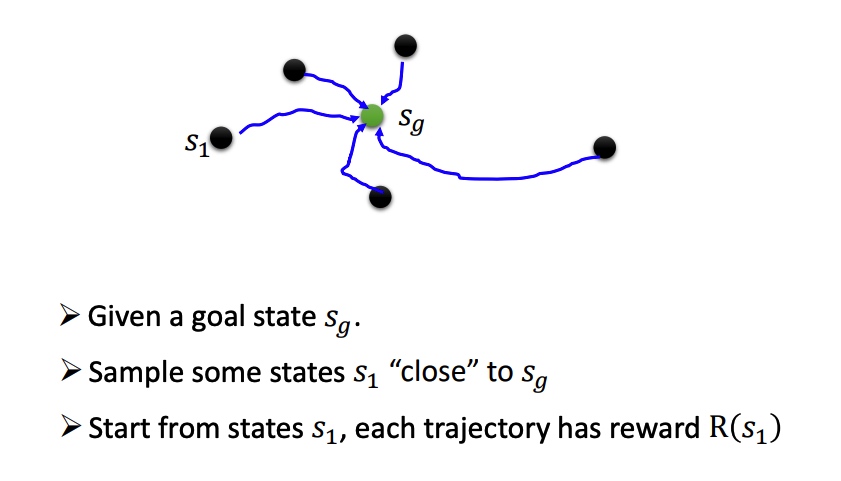
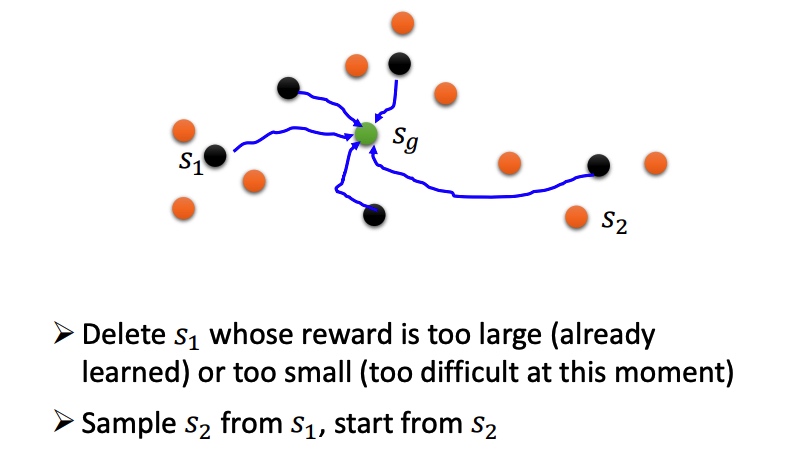
Hierarchical Reinforcement Learning
对 agent 分层,高层负责定目标,分配给底层 agent 执行。如果低一层的agent没法达到目标,那么高一层的agent会受到惩罚(高层agent将自己的愿景传达给底层agent)。
如果一个agent到了一个错误的目标,那就假设最初的目标本来就是一个错误的目标(保证已经实现的成果不被浪费)
我的笔记汇总:
- Policy Gradient、PPO: Proximal Policy Optimization、Q-Learning
- Actor Critic
- Sparse Reward
- Imitation Learning
Actor Critic
policy gradient
- 给定在某个 state 采取某个 action 的概率。
- baseline b 的作用是保证 reward 大的样本有更大的概率被采样到。
- 从当前时间点累加 reward,并且当前 action 对后面的 reward 影响很小,添加折扣系数。
- PG 效果受到采样数量和质量影响。

Q-learning
状态价值函数
状态行动价值函数
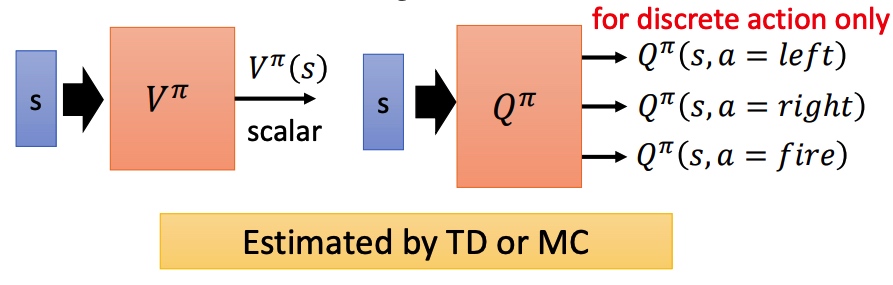
Actor-Critic
用 V 和 Q 替换 PG 中的累积 reward 和 baseline。新的模型需要训练两个网络,比较困难。
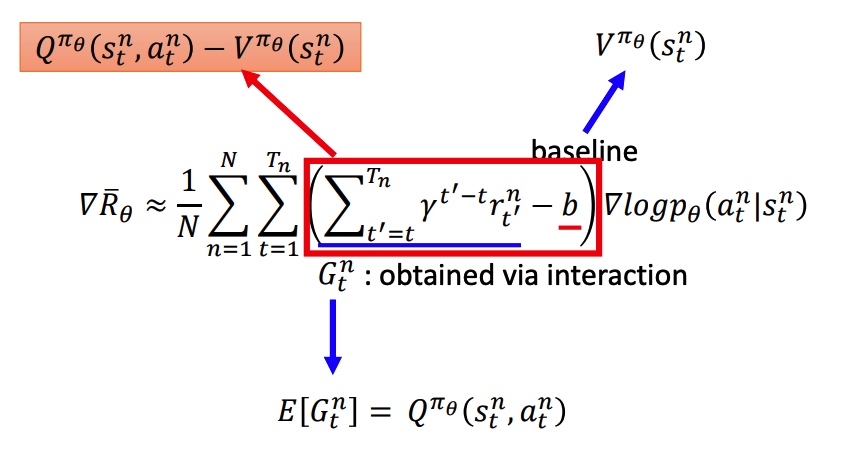
Advantage Actor-Critic
用 V 去替代 Q,能降低模型整体方差(MC 到 TD)。最下面两个公式转化是由实验得到。

训练过程:
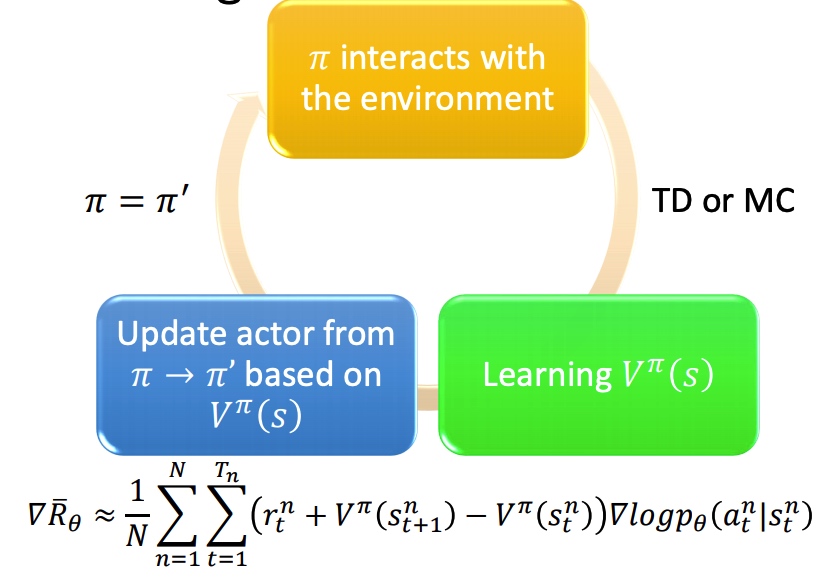
tip:
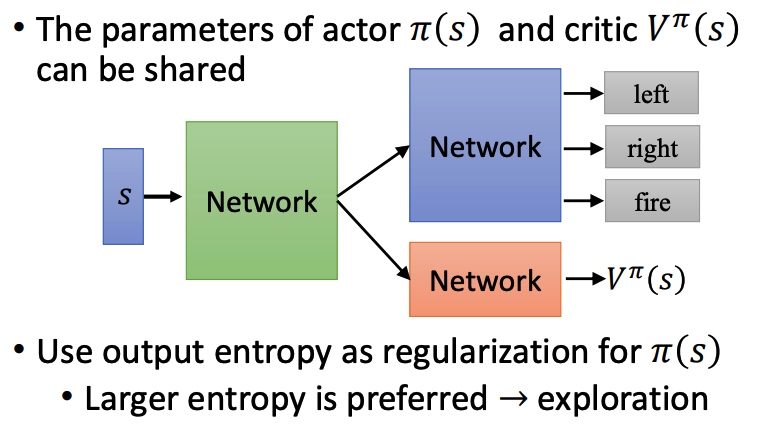
- actor 和 critic 具有相同的输入 s,可以共享部分网络结构。
- output entropy 作为 pi 的正则项,entropy 越大采样效果越好。
Asynchronous Advantage Acotr-Critic A3C
- 利用多个 worker 去训练。
- 每个 worker 复制主模型的参数。
- 每个模型单独采样,并且计算梯度。
- 更新全局参数。
Pathwise derivative policy gradient
该网络不仅仅告诉 actor 某一个 action 的好坏,还告诉 actor 应该返回哪一个 action。

将这个 actor 返回的 action 和 state 一起输入到一个固定的 Q,利用梯度上升更新 actor。
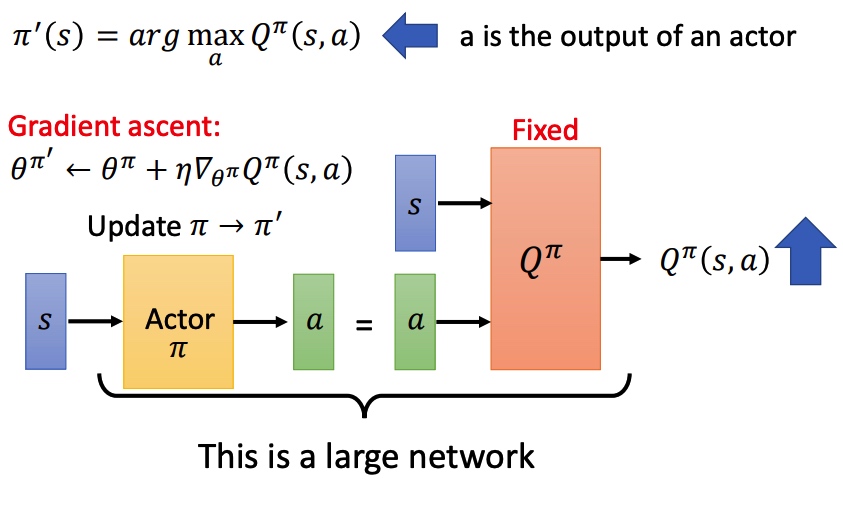
完整的训练过程和 conditional GAN 类似, actor 是 generator,Q 是 discriminator。
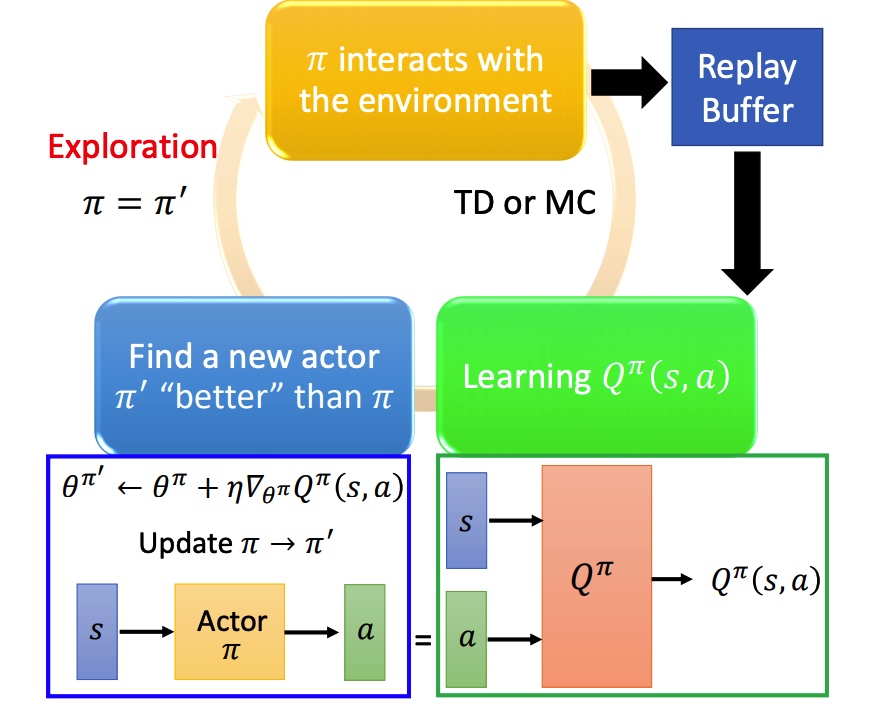
算法:
- action 由训练的 actor 决定
- 利用 s 和 a 更新 Q

GAN 和 AC 方法对比

GBDT(Gradient Boosting Decision Tree) 从名字上理解包含三个部分:提升、梯度和树。它最早由 Freidman 在 greedy function approximation :a gradient boosting machine 中提出。很多公司线上模型是基于 GBDT+FM 开发的,我们 Leader 甚至认为 GBDT 是传统的机器学习集大成者。断断续续使用 GBDT 一年多后,大胆写一篇有关的文章和大家分享。
朴素的想法
假设有一个游戏:给定数据集 ,寻找一个模型,使得平方损失函数 最小。
如果你的朋友提供一个可以使用但是不完美的模型,比如
在如何不修改这个模型的参数情况下,提高模型效果?
一个简单的思路是:重新训练一个模型实现
换一个角度是用模型学习数据 。得到新的模型 。
其中 的部分被我们称之为残差,即之前的模型没有学习到的部分。重新训练模型 正是学习残差。如果多次执行上面的步骤,可以将流程描述成:
即 ,这也就是 GBDT 。
如何理解 Gradient Boosting Decision Tree ?
Gradient Boosting Decision Tree 简称 GBDT,最早由 Friedman 在论文《Greedy function approximation: a gradient boosting machine》中提出。简单从题目中理解包含三个部分内容:Gradient Descent、Boosting、Decision Tree。
Decision Tree 即决策树,利用超平面对特征空间划分来预测和分类,根据处理的任务不同分成两种:分类树和回归树。在 GBDT 算法中,用到的是 CART 即分类回归树。用数学语言来描述为 ,完成样本 到决策树叶子节点 的映射,并将该叶子节点的权重 赋给样本。CART 中每次通过计算 gain 值贪心来进行二分裂。
Boosting 是一种常用的集成学习方法(另外一种是 Bagging)。利用弱学习算法,反复学习,得到一系列弱分类器(留一个问题,为什么不用线性回归做为弱分类器)。然后组合这些弱分类器,构成一个强分类器。上面提到的模型 即是一种 boosting 思路,依次训练多个 CART 树 ,并通过累加这些树得到一个强分类器 。
为什么 GBDT 可行?
在 2 中我提到 GBDT 包括三个部分并且讲述了 Boosting 和 Decison Tree。唯独没有提到 Gradient Descent,GBDT 的理论依据却恰恰和它相关。
回忆一下,Gradient Descent 是一种常用的最小化损失函数 的迭代方法。
- 给定初始值
- 迭代公式:
- 将 在 处进行一阶泰勒展开:
- 要使 ,取
- 其中 是步长,可以通过 line search 确定,但一般直接赋一个很小的数。
在 1 中提到的问题中,损失函数是 MSE 。
我们的任务是通过调整 最小化 。
如果将 当成是参数,并对损失函数求导得到 。
可以发现,在 1 中提到的模型 学习的残差 正好等于负梯度,即 。
所以,参数的梯度下降和函数的梯度下降原理上是一致的:
GBDT 算法流程
模型 F 定义为加法模型:
其中,x 为输入样本,h 为分类回归树,w 是分类回归树的参数, 是每棵树的权重。
通过最小化损失函数求解最优模型:
输入:
- 初始化:
- 对于 :
- 计算负梯度(伪残差):
- 根据 学习第 m 棵树:
- line searcher 找步长:
- 令 ,更新模型:
- 输出
说明:
- 初始化 方法
- 求解损失函数最小
- 随机初始化
- 训练样本的充分统计量
- 每一轮拟合负梯度,而不是拟合残差,是为方便之后扩展到其他损失函数。
- 最小化问题中,如果有解析解,直接带入。否则,利用泰勒二阶展开,Newton Step 得到近似解。
这一篇就先到这里,之后还会分享 GBDT 常用损失函数推导以及 XGboost 相关内容。如果有任何想法,都可以在留言区和我交流。
Reference
- 李航, 《统计学习方法》8.4 提升树
- Freidman,greedy function approximation :a gradient boosting machine
- 【19年ML思考笔记】GBDT碎碎念(1)谈回归树的分裂准则 - 知乎
- 机器学习-一文理解GBDT的原理-20171001 - 知乎
- GBDT入门详解 - Scorpio.Lu|Blog
- python - Why Gradient Boosting not working in Linear Regression? - Stack Overflow
- GBDT基本原理及算法描述 - Y学习使我快乐V的博客 - CSDN博客
- GBDT的那些事儿 - 知乎
(FTRL) Follow The Regularized Leader
FTRL 是 Google 提出的一种优化算法。常规的优化方法例如梯度下降、牛顿法等属于批处理算法,每次更新需要对 batch 内的训练样本重新训练一遍。在线学习场景下,我们希望模型迭代速度越快越好。例如用户发生一次点击行为后,模型就能快速进行调整。FTRL 在这个场景中能求解出稀疏化的模型。
基础知识
- L1 正则比 L2 正则可以产生更稀疏的解。
- 次梯度:对于 L1 正则在 处不可导的情况,使用次梯度下降来解决。次梯度对应一个集合 ,集合中的任意一个元素都能被当成次梯度。以 L1 正则为例,非零处梯度是 1 或 -1,所以 处的次梯度可以取 之内任意一个值。
FTL
FTL(Follow The Leader) 算法:每次找到让之前所有损失函数之和最小的参数。
FTRL 中的 R 是 Regularized,可以很容易猜出来在 FTL 的基础上加正则项。
代理函数
FTRL 的损失函数直接很难求解,一般需要引入一个代理损失函数 。代理损失函数常选择比较容易求解析解以及求出来的解和优化原函数得到的解差距不能太大。
我们通过两个解之间的距离 Regret 来衡量效果:
其中 是直接优化 FTRL 算法得到的参数。当距离满足 ,损失函数认为是有效的。其物理意义是,随着训练样本的增加,两个优化目标优化出来的参数效果越接近。
推导过程
参数 的迭代公式:
其中 , 为 的次梯度。参数 ,学习率 ,随着迭代轮数增加而减少。
展开迭代公式
其中 。
对 求偏导得到:
和 异号时,等式成立。
根据基础知识里面提到的对于 L1 正则利用偏导数代替无法求解的情况,得到:
- 当 时, ,
- 当 时, ,
- 当 时,当且仅当 成立
因此可得:
FTRL 和 SGD 的关系
将 SGD 的迭代公式写成:
FTRL 迭代公式为:
代入 到上面的公式中,得到
求偏导得到
令偏导等于 0 :
化简得到:
代入 :
根据上一个公式得出上一轮的迭代公式:
两式相减:
最终化简得到和 SGD 迭代公式相同的公式:
FTRL 工程化伪代码
引用自论文 Ad Click Prediction: a View from the Trenches
下面的伪代码中学习率和前面公式推导时使用的一些不一样: 。Facebook 在 GBDT + LR 的论文中研究过不同的学习率影响,具体可以参看博文 Practical Lessons from Predicting Clicks on Ads at Facebook(gbdt + lr) | 算法花园。

例:FM 使用 FTRL 优化
FM 是工业界常用的机器学习算法,在之前博文 (FM)Factorization Machines 中有简单的介绍。内部的 FTRL+FM 代码没有开源,所以也不好分析。从 FM+FTRL算法原理以及工程化实现 - 知乎 中找了一张 FTRL+FM 的伪代码图片。

Reference
Info
课件下载:Hung-yi Lee - Deep Reinforcement Learning
课程视频:DRL Lecture 1: Policy Gradient (Review) - YouTube
- Change Log
- 20191226: 整理 PPO 相关资料
- 20191227: 整理 Q-Learning 相关资料
- 20200906: 拖延半年多没有整理笔记,将剩下的内容整理到单独的笔记中。
我的笔记汇总:
- Policy Gradient、PPO: Proximal Policy Optimization、Q-Learning
- Actor Critic
- Sparse Reward
- Imitation Learning
RL 基础
强化学习基本定义:
- Actor:可以感知环境中的状态,通过执行不同的动作得到反馈的奖励,在此基础上进行学习优化。
- Environment:指除 Actor 之外的所有事务,受 Actor 动作影响而改变其状态,并给 Actor 对应的奖励。
- on-policy 和 off-policy 的区别在于 Actor 和 Environment 交互的策略和它自身在学习的策略是否是同一个。
一些符号:
- State s 是对环境的描述,其状态空间是 S。
- Action a 是 Actore 的行为描述,其动作空间是 A。
- Policy 代表在给定环境状态 s 下 动作 a 的分布。
- Reward 在状态 s 下执行动作 a 后,Env 给出的打分。
Policy Gradient
Policy Network 最后输出的是概率。
目标:调整 actor 中神经网络 policy ,得到 ,最大化 reward。
trajectory 由一系列的状态和动作组成,出现这种组合的概率是 。
reward :根据 s 和 a 计算得分 r,求和得到 R。在围棋等部分任务中,无法获得中间的 r(下完完整的一盘棋后能得到输赢的结果)。
需要计算 R 的期望 ,形式和 GAN 类似。如果一个动作得到 reward 多,那么就增大这个动作出现的概率。最终达到 agent 所做 policy 的 reward 一直都比较高。
强化学习中,没有 label。需要从环境中采样得到 和 R,根据下面的公式去优化 agent。相当于去求一个 likelihood。
,这一步中用到对 log 函数进行链式求导。
参数更新方法:
- 在环境中进行采样,得到一系列的轨迹和回报。
- 利用状态求梯度,更新模型。如果 R 为正,增大概率 , 否则减少概率。
- 重复上面的流程。

PG 的例子
训练 actor 的过程看成是分类任务:输入 state ,输出 action。
最下面公式分别是反向传播梯度计算和 PG 的反向梯度计算,PG 中要乘以整个轨迹的 R。
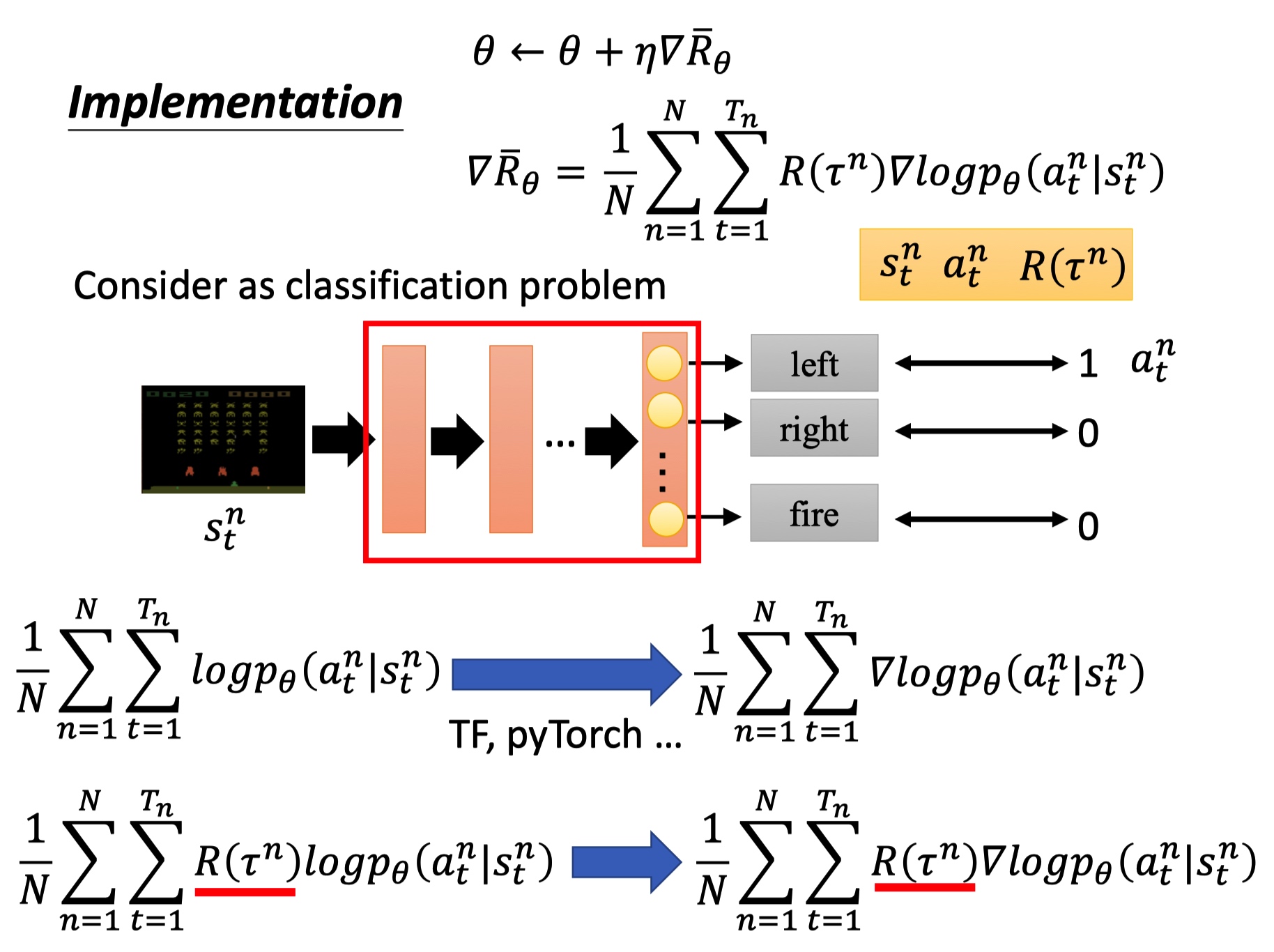
tip 1: add a baseline
强化学习的优化和样本质量有关,避免采样不充分。Reawrd 函数变成 R-b,代表回报小于 b 的都被我们当成负样本,这样模型能去学习得分更高的动作。b 一般可以使用 R 的均值。
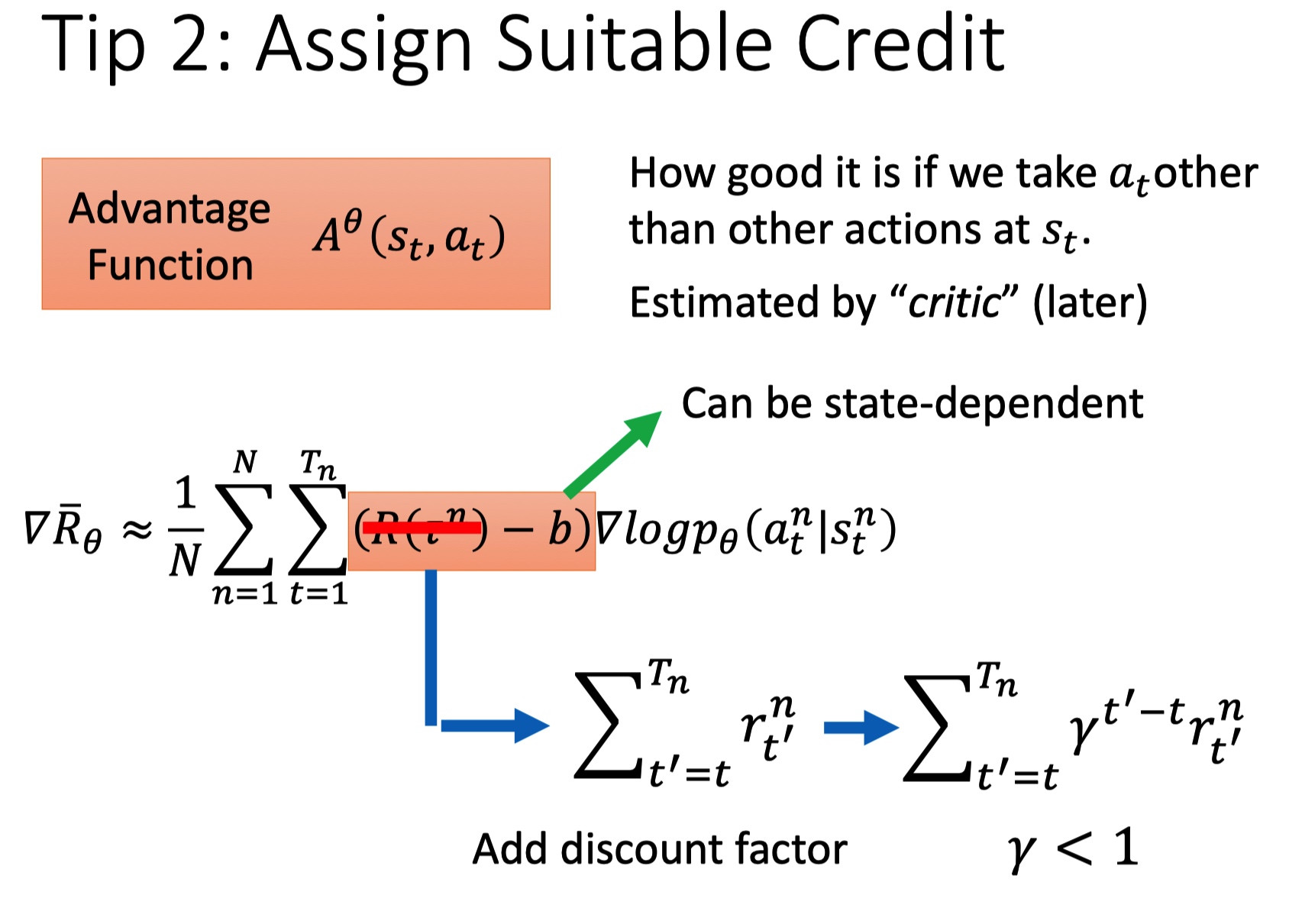
tip 2: assign suitable credit
一场游戏中,不论动作好坏,总会乘上相同的权重 R,这种方法是不合理的,希望每个 action 的权重不同。
- 引入一个 discount rate,对 t 之后的动作 r 进行降权重。
- 利用 Advantage Function 评价状态 s 下动作 a 的好坏 critic。
PPO: Proximal Policy Optimization
importance sampling
假设需要估计期望 ,x 符合 p 分布,将期望写成积分的形式。由于在 P 分布下面很难采样,把问题转化到已知 q 分布上,得到在 p 分布下计算期望公式。
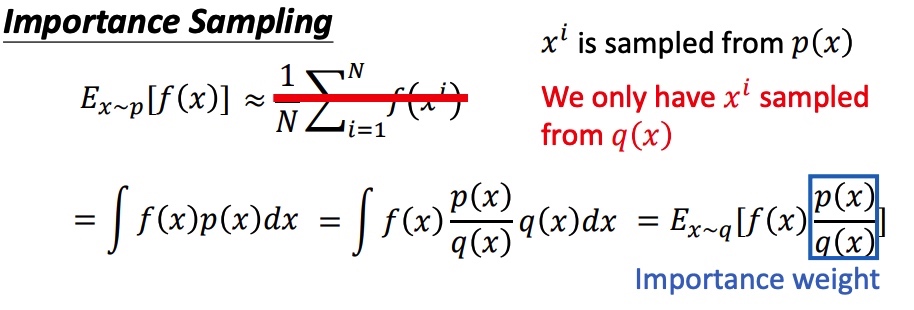
上面方法得到 p 和 q 期望接近,但是方差可能相差很大,且和 有关。
原分布的方差:
新分布的方差:
在 p 和 q 分布不一致时,且采样不充分时,可能会带来比较大的误差。
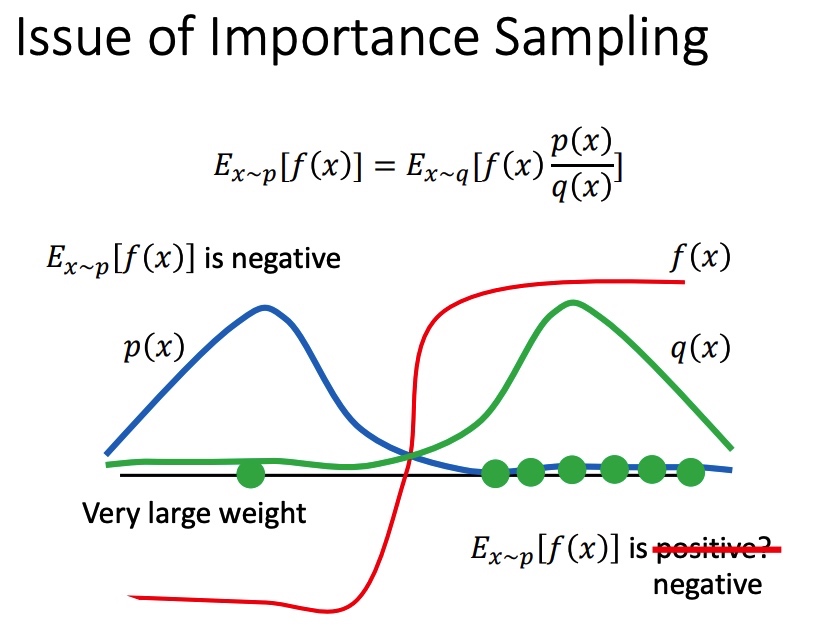
从 On-policy 到 Off-policy
on-policy 时,PG 每次参数更新完成后,actor 就改变了,不能使用之前的数据,必须和环境重新互动收集数据。引入 进行采样,就能将 PG 转为 off-ploicy。

和之前相比,相当于引入重要性采样,所以也有前一节中提到的重要性采样不足问题。
PPO/TRPO
为了克服采样的分布与原分布差距过大的不足,PPO 引入 KL 散度进行约束。KL 散度用来衡量两个分布的接近程度。
TRPO(Trust Region Policy Optimization),要求 。
KL 散度可能比较难计算,在实际中常使用 PPO2。
- A>0,代表当前策虑表现好。需要增大 ,通过 clip 增加一个上限,防止 和旧分布变化太大。
- A<0,代表当前策虑表现差,不限制新旧分布的差异程度,只需要大幅度改变 。

PPO algorithm
系数 在迭代的过程中需要进行动态调整。引入 ,KL > KLmax,说明 penalty 没有发挥作用,增大 。

Q-Learning
value-base 方法,利用 critic 网络评价 actor 。通过状态价值函数 来衡量预期的期望。V 和 pi、s 相关。
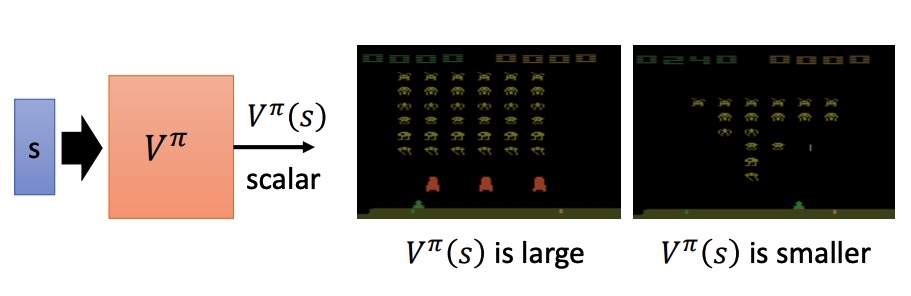
- Monte-Carlo MC: 训练网络使预测的 和实际完整游戏 reward 接近。
- Temporal-difference TD: 训练网络尽量满足 等式,两个状态之间的收益差。
MC: 根据策虑 进行游戏得到最后的 ,最终存在方差大的问题。
TD: r 的方差比较小, 在采样不充分的情况下,可能不准确。

Another Critic
State-action value function :预测在 pi 策略下,pair(s, a) 的值。相当于假设 state 情况下强制采取 action a。
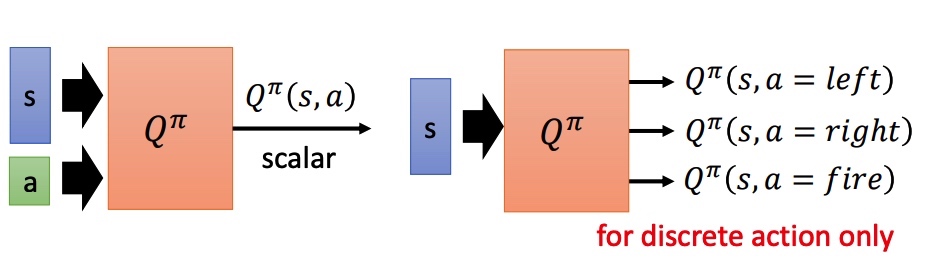
对于非分类的方法:
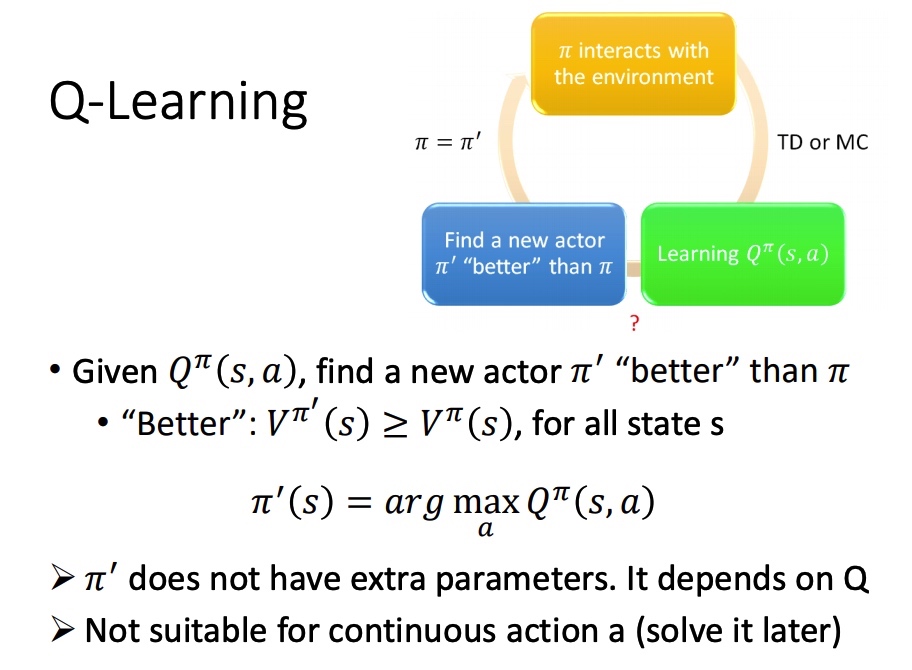
Q-Learning
- 初始 actor 与环境互动
- 学习该 actor 对应的 Q function
- 找一个比 好的策虑:,满足 ,
在给定 state 下,分别代入 action,取函数值最大的 a,作为后面对该 state 时采取的 action。
证明新的策虑存在:

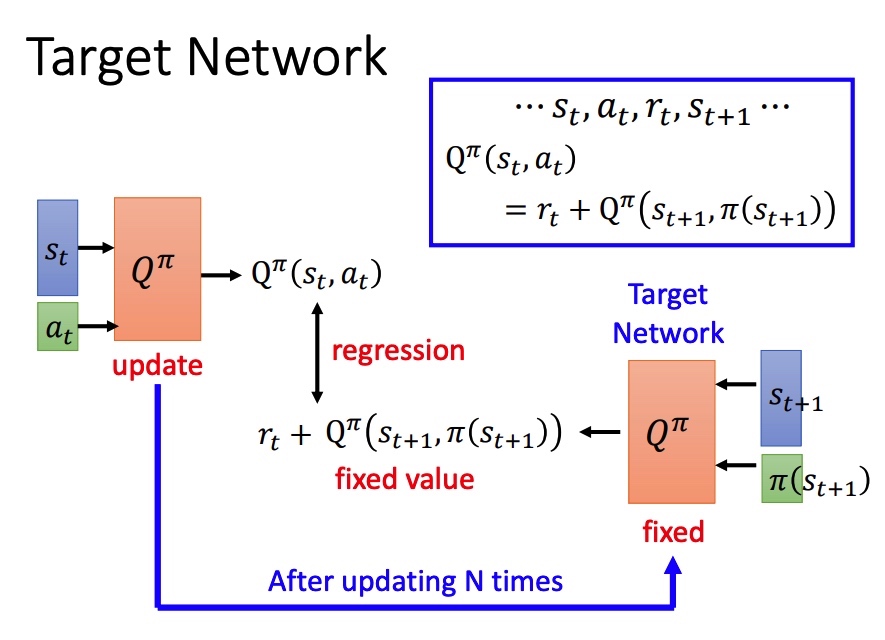
Target NetWork
左右两边的网络相同,如果同时训练比较困难。简单的想法是固定右边的网络进行训练,一定次数后再拷贝左边的网络。
Exploration
Q function 导致 actor 每次都会选择具有更大值的 action,无法准确估计某一些动作,对于收集数据而言是一个弊端。
- Epsilon Greedy
- 小概率进行损失采样
- Boltzmann Exploration
- 利用 softmax 计算选取动作的概率,然后进行采样

Replay buffer
采样之后的 保存在一个 buffer 里面(可能是不同策虑下采样得到的),每次训练从 buffer 中 sample 一个 batch。
结果:训练方法变成 off-policy。减少 RL 重复采样,充分利用数据。
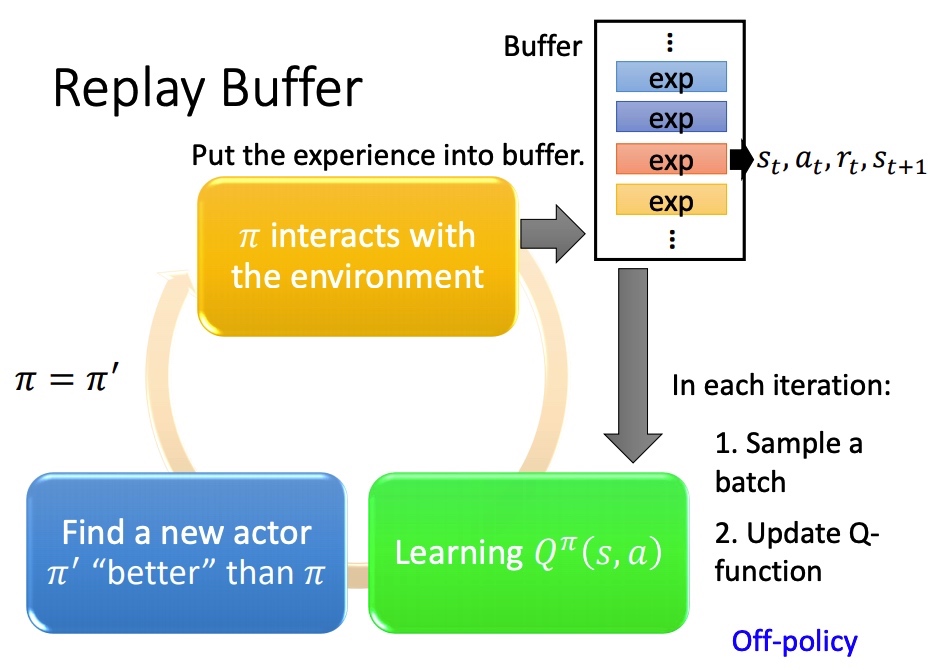
Typical Q-Learning Algorithm
Q-Learning 流程:

Double DQN DDQN
- Q value 容易高估:目标值 倾向于选择被高估的 action,导致 target 很大。
- 选动作的 Q’ 和计算 value 的 Q(target network) 不同。Q 中高估 a,Q’ 可能会准确估计 V 值。Q’ 中高估 a ,可能不会被 Q 选中。

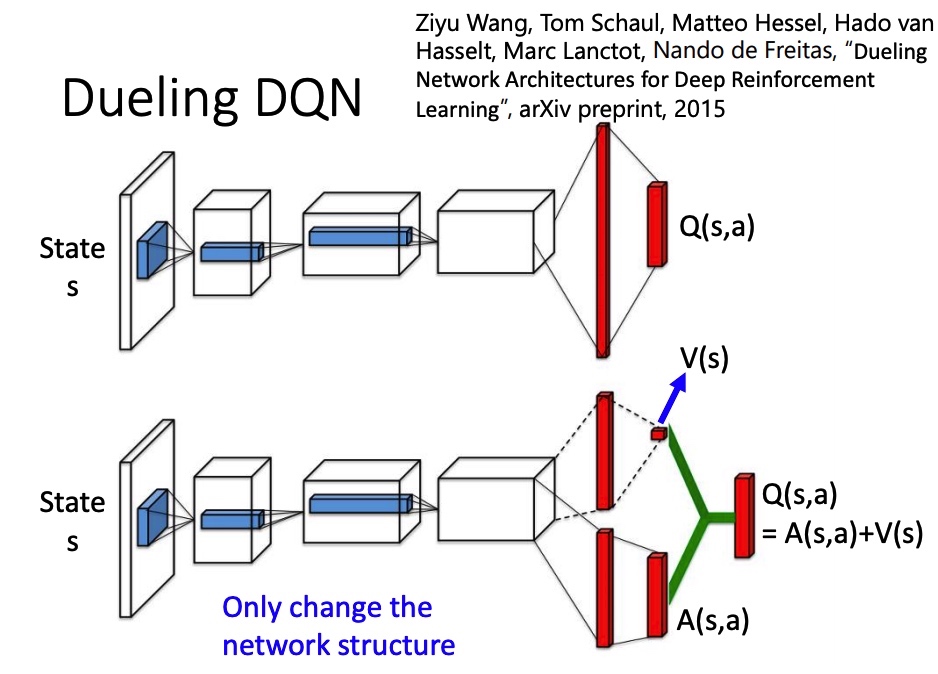
Dueling DQN
改 network 架构。V(s) 代表 s 所具有的价值,不同的 action 共享。 A(s,a) advantage function 代表在 s 下执行 a 的价值。最后 。
为了让网络倾向于使用 V(能训练这个网络),得到 A 后,要对 A 做 normalize。
Prioritized Reply
在训练过程中,对于经验 buffer 里面的样本,TD error 比较大的样本有更大的概率被采样,即难训练的数据增大被采样的概率。
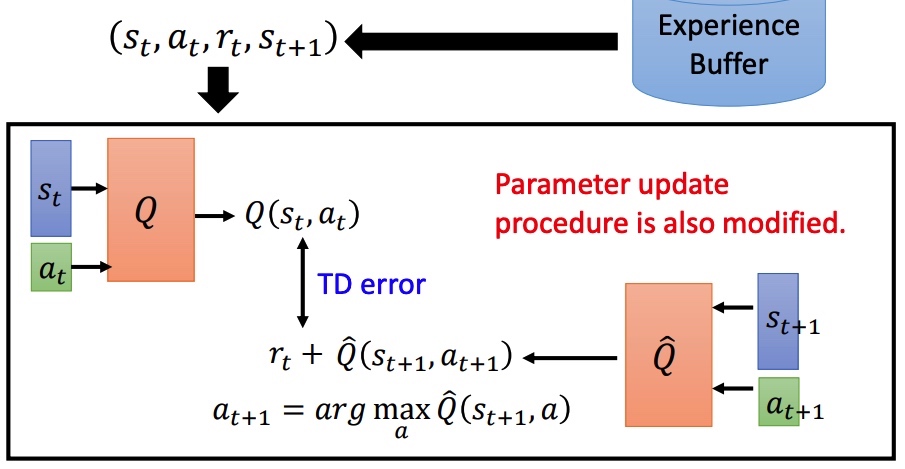
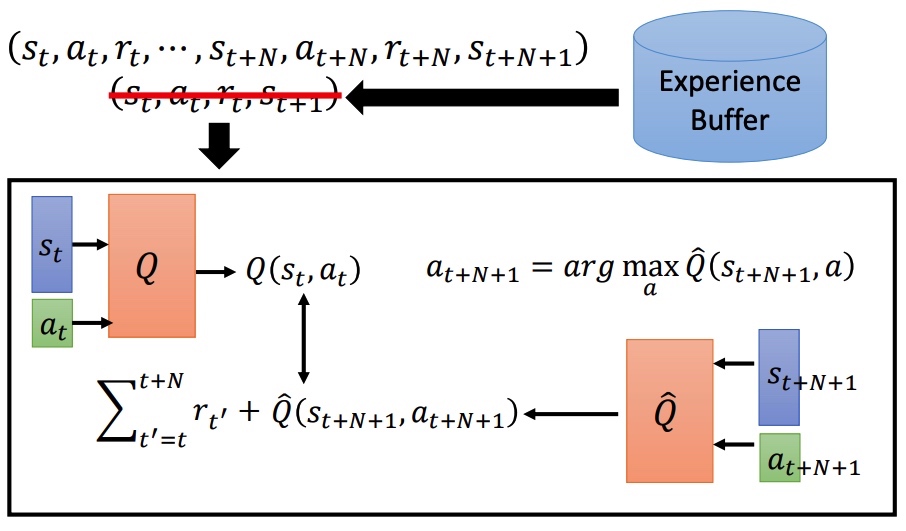
Multi-step
综合 MC 和 TD 的优点,训练样本按一定步长 N 进行采样。MC 准确方差大,TD 方差小,估计不准。
Noisy Net

- Noise on Action:在相同状态下,可能会采取不同的动作。
- Noise on Parameters:开始时加入噪声。同一个 episode 内,参数不会改变。相同状态下,动作相同。
更好探索环境。
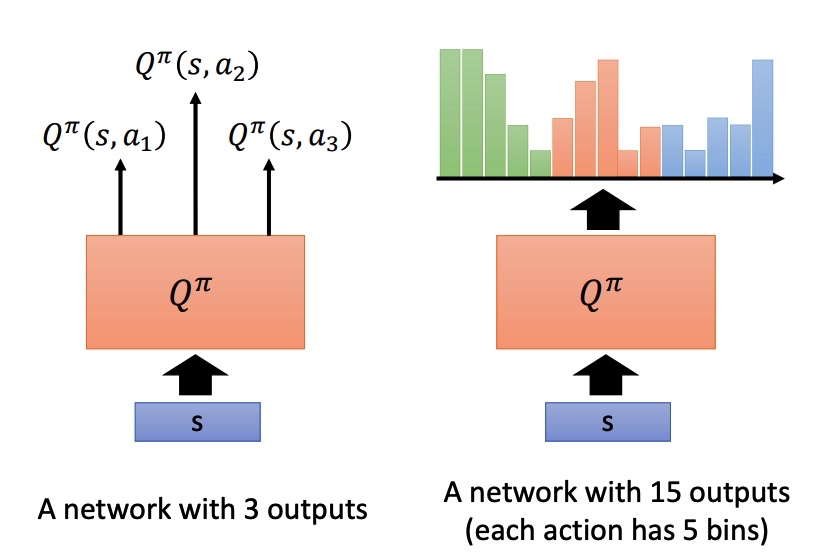
Distributional Q-function
Q 是累积收益的期望,实际上在 s 采取 a 时,最终所有得到的 reward 为一个分布 reward distribution。部分时候分布不同,可能期望相同,所以用期望来代替 reward 会损失一些信息。
Distributional Q-function 直接输出分布,均值相同时,采取方差小的方案。这种方法不会产生高估 q 值的情况。
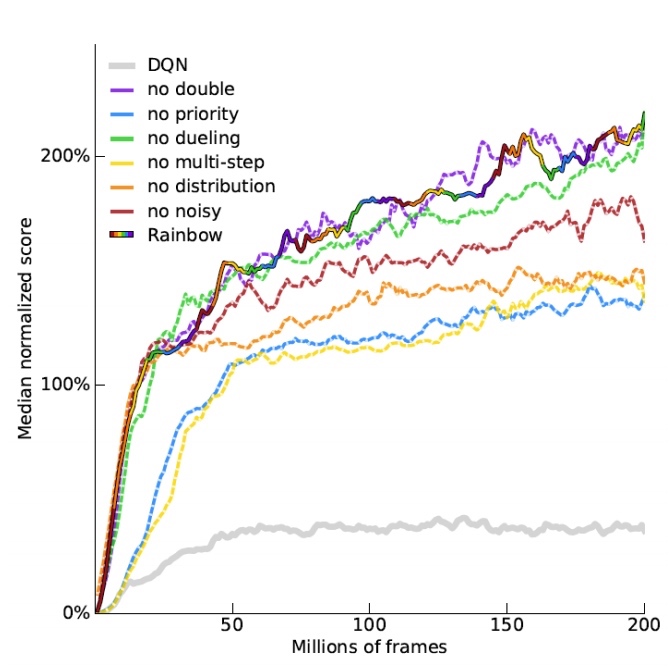
Rainbow
rainbow 是各种策略的混合体。
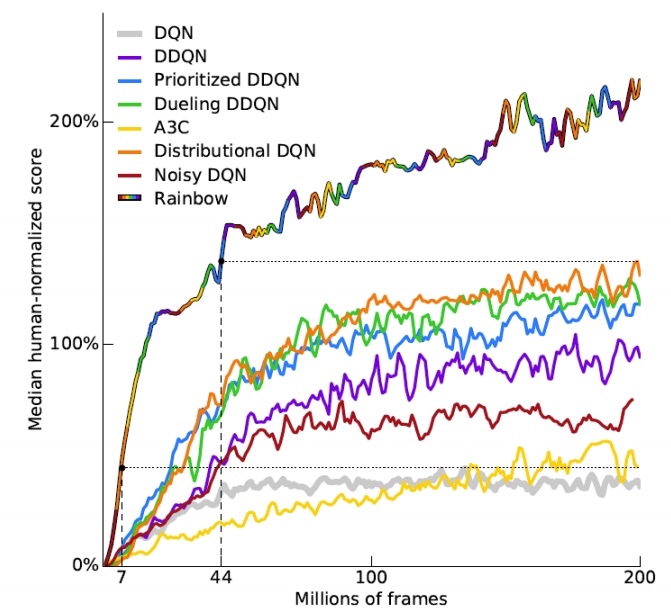
DDQN 影响不大。
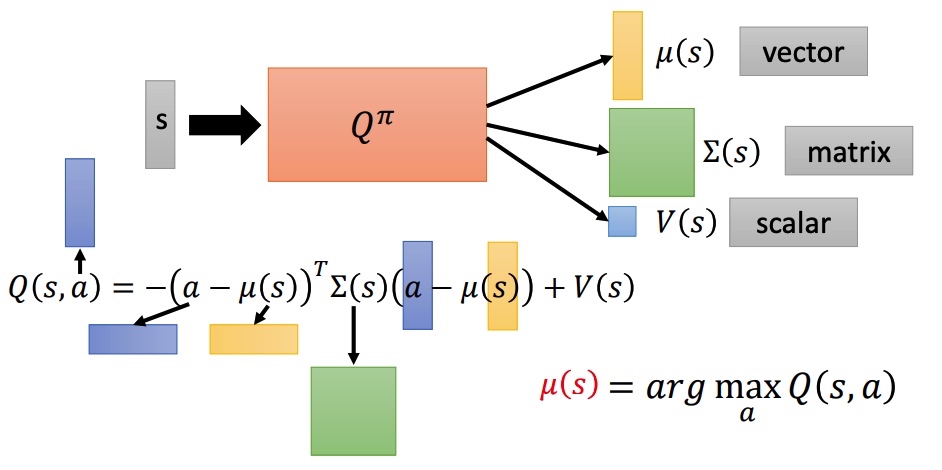
Continuous Actions
action 是一个连续的向量,Q-learning 不是一个很好的方法。
- 从 a 中采样出一批动作,看哪个行动 Q 值最大。
- 使用 gradient ascent 解决最优化问题。
- 设计一个网络来化简过程。
- 和 是高斯分布的方差和均值,保证矩阵一定是正定。
- 最小化下面的函数,需要最小化 。
Reference
去年学习这门做的部分笔记,现在分享出来。
笔记格式有些问题,持续整理中。
- 大量内容参考 mbadry1/CS231n-2017-Summary
Table of contents
- Table of contents
- Course Info
- 01. Introduction to CNN for visual recognition
- 02. Image classification
- 03. Loss function and optimization
- 04. Introduction to Neural network
- 05. Convolutional neural networks (CNNs)
- 06. Training neural networks I
- 07. Training neural networks II
- 09. CNN architectures
- Reference
Course Info
- 主页: http://cs231n.stanford.edu/
- 视频:斯坦福深度学习课程CS231N 2017中文字幕版+全部作业参考_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili
- 大纲:Syllabus | CS 231N
- 课件:Index of /slides/2017
- 笔记:贺完结!CS231n官方笔记授权翻译总集篇发布
- 作业仓库:MachineLearning/CS231n at master · xiang578/MachineLearning
- 总课时: 16
01. Introduction to CNN for visual recognition
- 视觉地出现促进了物种竞争。
- ImageNet 是由李飞飞维护的一个大型图像数据集。
- 自从 2012 年 CNN 出现之后,图像分类的错误率大幅度下降。 神经网络的深度也从 7 层增加到 2015 年的 152 层。截止到目前,机器分类准确率已经超过人类,所以 ImageNet 也不再举办相关比赛。
- CNN 在 1998 年就被提出,但是这几年才流行开来。主要原因有:1) 硬件发展,并行计算速度提到 2)大规模带标签的数据集。
- Gola: Understand how to write from scratch, debug and train convolutional neural networks.
02. Image classification
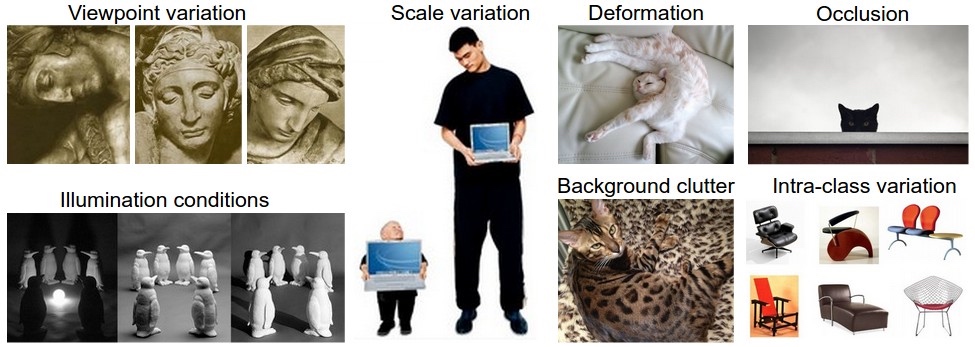
- 图像由一大堆没有规律的数字组成,无法直观的进行分类,所以存在语义鸿沟。分类的挑战有:视角变化、大小变化、形变、遮挡、光照条件、背景干扰、类内差异。
- Data-Driven Approach
- Collect a dataset of images and labels
- Use Machine Learning to train a classifier
- Evaluate the classifier on new images
- 图像分类流程:输入、学习、评估
- 图像分类数据集:CIFAR-10,这个数据集包含了60000张32X32的小图像。每张图像都有10种分类标签中的一种。这60000张图像被分为包含50000张图像的训练集和包含10000张图像的测试集。
- 一种直观的图像分类算法:K-nearest neighbor(knn)
- 为每一张需要预测的图片找到距离最近的 k 张训练集中的图片,然后选着在这 k 张图片中出现次数最多的标签做为预测图片的标签(多数表决)。
- 训练过程:记录所有的数据和标签
- 预测过程:预测给定图片的标签
- Hyperparameters:k and the distance Metric
- Distance Metric
- L1 distance(Manhattan Distance)
- L2 distance(Euclidean Distance)
- knn 缺点
- Very slow at test time
- Distance metrics on pixels are not informative
- 反例:下面四张图片的 L2 距离相同
- Hyperparameters: choices about the algorithm that we set ranther than learn
- 留一法 Setting Hyperparameters by Cross-validation:
- 将数据划分为 f 个集合以及一个 test 集合,数据划分中药保证数据集的分布一致。
- 给定超参数,利用 f-1 个集合对算法进行训练,在剩下的一个集合中测试训练效果,重复这一个过程,直到所有的集合都当过测试集。
- 选择在训练集中平均表现最好的超参数。
- Linear classification:
Y = wX + b- b 为 bias,调节模型对结果的偏好
- 通过最小化损失函数来,来确定 w 和 b 的值。
- Linear SVM: classifier is an option for solving the image classification problem, but the curse of dimensions makes it stop improving at some point. @todo
- Logistics Regression: 无法解决非线性的图像数据
03. Loss function and optimization
- 通过 Loss function 评估参数质量
- 比如 $$L=\frac{1}{N}\sum_iL_i\left(f\left(x_i,W\right),y_i\right)$$
- Multiclass SVM loss 多分类支持向量机损失函数
-
- 这种损失函数被称为合页损失 Hinge loss
- SVM 的损失函数要求正确类别的分类分数要比其他类别的高出一个边界值。
- L2-SVM 中使用平方折叶损失函数$$\max(0,-)^2$$能更强烈地惩罚过界的边界值。但是选择使用哪一个损失函数需要通过实验结果来判断。
- 举例

- 根据上面的公式计算:$$L = \max(0,437.9-(-96.8)) + \max(0,61.95-(-96.8))=695.45$$
- 猫的分类得分在三个类别中不是最高得,所以我们需要继续优化。
-
- Suppose that we found a W such that L = 0. Is this W unique?
- No! 2W is also has L = 0!
- Regularization: 正则化,向某一些特定的权值 W 添加惩罚,防止权值过大,减轻模型的复杂度,提高泛化能力,也避免在数据集中过拟合现象。
-
R正则项 $$\lambda$$ 正则化参数
-
- 常用正则化方法
- L2$$\begin{matrix} R(W)=\sum_{k}\sum_l W^2_{k,l} \end{matrix}$$
- L1$$\begin{matrix} R(W)=\sum_{k}\sum_l \left\vert W_{k,l} \right\vert \end{matrix}$$
- Elastic net(L1 + L2): $$\begin{matrix} R(W)=\sum_{k}\sum_l \beta W^2_{k,l} + \left\vert W_{k,l} \right\vert \end{matrix}$$
- Dropout
- Batch normalization
- etc
- L2 惩罚倾向于更小更分散的权重向量,L1 倾向于稀疏项。
- Softmax function:
-
- 该分类器将输出向量 f 中的评分值解释为没有归一化的对数概率,通过归一化之后,所有概率之和为1。
- Loss 也称交叉熵损失 cross-entropy loss $$L_i = - \log\left(\frac{e^{s_i}}{\sum e^{s_j}}\right)$$
-
1 | f = np.array([123, 456, 789]) # 例子中有3个分类,每个评分的数值都很大 |
- SVM 和 Softmax 比较
- 评分,SVM 的损失函数鼓励正确的分类的分值比其他分类的分值高出一个边界值。
- 对数概率,Softmax 鼓励正确的分类归一化后的对数概率提高。
- Softmax 永远不会满意,SVM 超过边界值就满意了。
- Optimization:最优化过程
- Follow the slope
- Follow the slope
- 梯度是函数的斜率的一般化表达,它不是一个值,而是一个向量,它是各个维度的斜率组成的向量。
- Numerical gradient: Approximate, slow, easy to write. (But its useful in debugging.)
- Analytic gradient: Exact, Fast, Error-prone. (Always used in practice)
- 实际应用中使用分析梯度法,但可以用数值梯度法去检查分析梯度法的正确性。
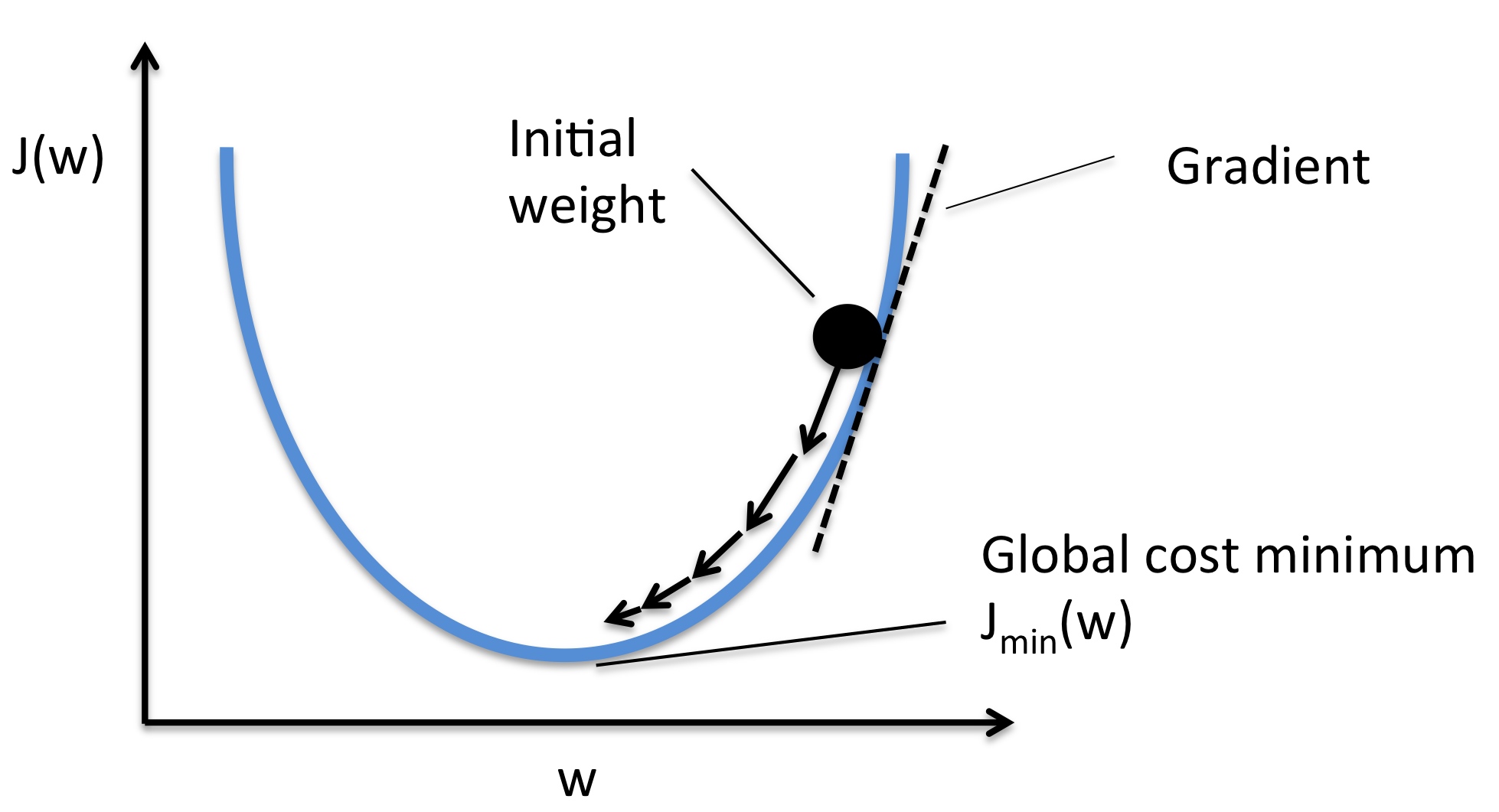
- 利用梯度优化参数的过程:
W = W - learning_rate * W_grad - learning_rate 被称为是学习率,是一个比较重要的超参数
- Stochastic Gradient Descent SGD 随机梯度下降法
- 每次使用一小部分的数据进行梯度计算,这样可以加快计算的速度。
- 每个批量中只有1个数据样本,则被称为随机梯度下降(在线梯度下降)
- 图像分类任务中三大关键部分:
- 评分函数
- 损失函数:量化某个具体参数 的质量
- 最优化:寻找能使得损失函数值最小化的参数 的过程
04. Introduction to Neural network
- 反向传播:在已知损失函数 的基础上,如何计算导数?
- 计算图
- 由于计算神经网络中某些函数的梯度很困难,所以引入计算图的概念简化运算。
- 在计算图中,对应函数所有的变量转换成为计算图的输入,运算符号变成图中的一个节点(门单元)。
- 反向传播:从尾部开始,根据链式法则递归地向前计算梯度,一直到网络的输入端。
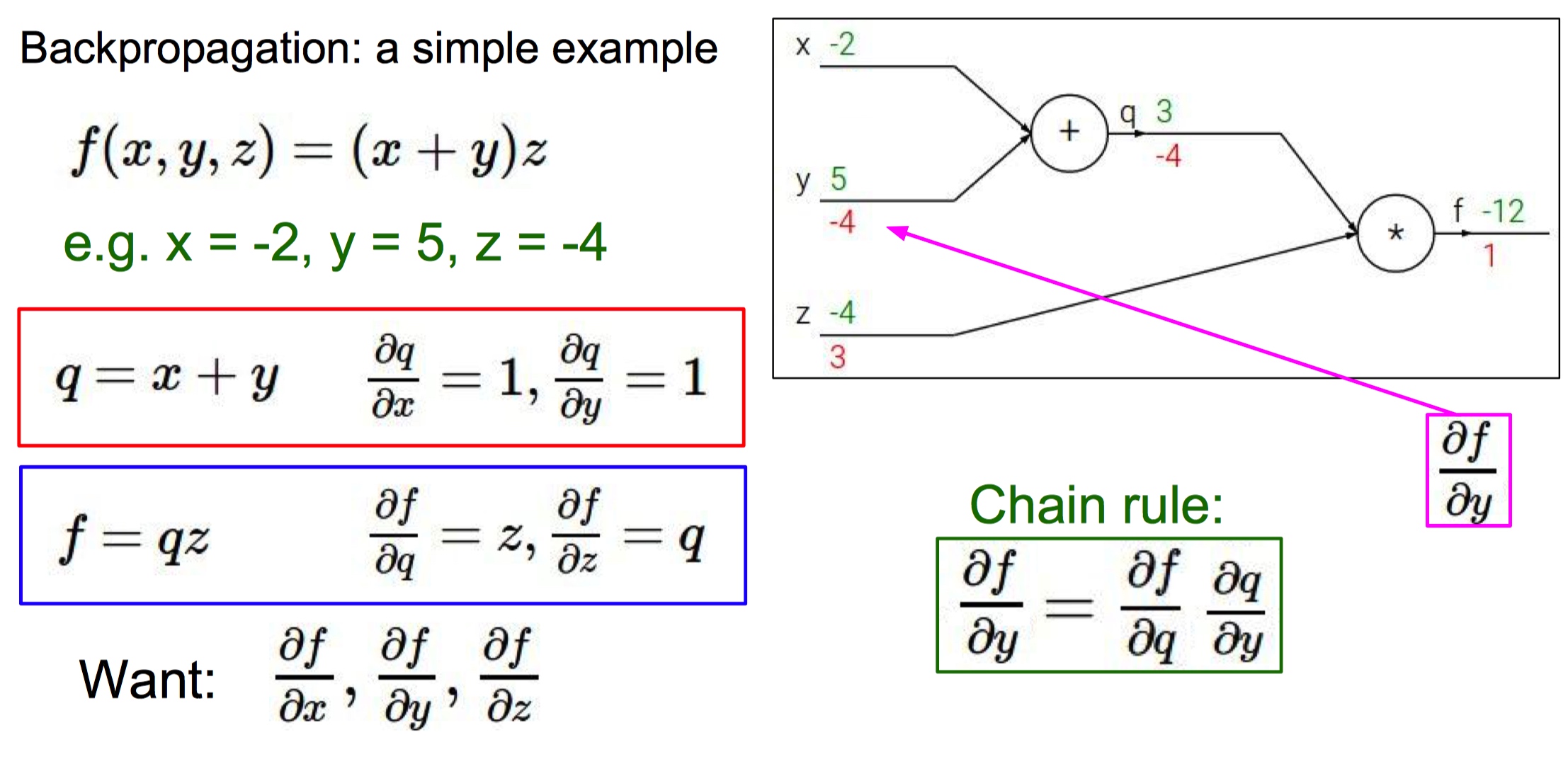
- 绿色是正向传播,红色是反向传播。
- 对于计算图中的每一个节点,我们需要计算这个节点上的局部梯度,之后根据链式法则反向传递梯度。
- Sigmoid 函数:
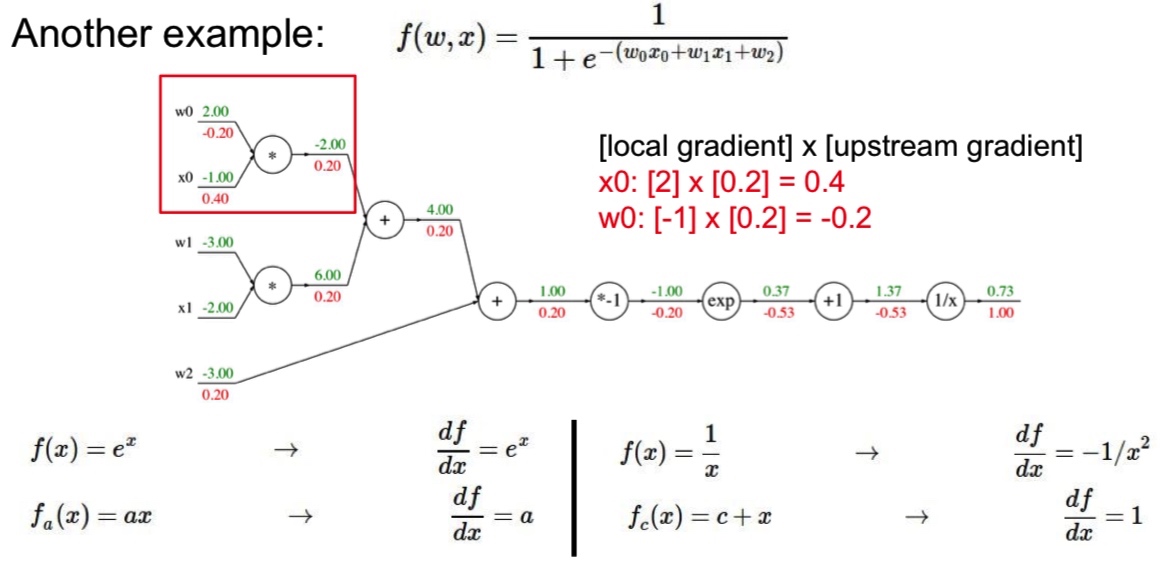
- 对于门单元 ,求导的结果是 ,输入为 1.37,梯度返回值为 1.00,所以这一步中的梯度是 。
- 模块化思想:对 求导的结果是 。如果 sigmoid 表达式输入值为 1.0 时,则前向传播中的结果是 0.73。根据求导结果计算可得局部梯度是 。
- Modularized implementation: forward/backwar API
1 | class MultuplyGate(object): |
- 深度学习框架中会实现的门单元:Multiplication、Max、Plus、Minus、Sigmoid、Convolution
- 常用计算单元
- **加法门单元:**把输出的梯度相等地分发给它所有的输入,这一行为与输入值在前向传播时的值无关。
- **取最大值门单元:**将梯度转给前向传播中值最大的那个输入,其余输入的值为0。
- **乘法门单元:**等值缩放。局部梯度就是输入值,但是需要相互交换,然后根据链式法则乘以输出值得梯度。
- Neural NetWorks
- (Before) Linear score function $$f = Wx$$
- (Now) 2-layer Neural NetWork $$f=W_2\max(0,W_1x)$$
- ReLU $$\max(0,x)$$ 是激活函数,如果不使用激活函数,神经网络只是线性模型的组合,无法拟合非线性情况。
- 神经网络是更复杂的模型的基础组件
05. Convolutional neural networks (CNNs)
- 这一轮浪潮的开端:AlxNet
- 卷积神经网络
- Fully Connected Layer 全连接层:这一层中所有的神经元链接在一起。
- Convolution Layer:
- 通过参数共享来控制参数的数量。Parameter sharing
- Sparsity of connections
- 卷积神经网络能学习到不同层次的输入信息
- 常见的神经网络结构:
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC - 使用小的卷积核大小的优点:多个卷积层与非线性的激活层交替的结构,比单一卷积层的结构更能提取出深层的更好地特征。而且使用的参数也会更少
- 计算卷积层输出
- stride 是卷积核在移动时的步长
- 通用公式 (N-F)/stride + 1
- stride 1 => (7-3)/1 + 1 = 5
- stride 2 => (7-3)/2 + 1 = 3
- stride 3 => (7-3)/3 + 1 = 2.33
- Zero pad the border: 用零填充所有的边界,保证输入输出图像大小相同,保留图像边缘信息,提高算法性能
- 步长为 1 时,需要填充的边界计算公式:(F-1)/2
- F = 3 => zero pad with 1
- F = 5 => zero pad with 2
- F = 7 => zero pad with 3
- 步长为 1 时,需要填充的边界计算公式:(F-1)/2
- 计算例子
- 输入大小
32*32*3卷积大小 10 5*5 stride 1 pad 2 - output
32*32*10 - 每个 filter 的参数数量:
5*5*3+1 =76bias - 全部参数数量 76*10=760
- 输入大小
- 卷积常用超参数设置
- 卷积使用小尺寸滤波器
- 卷积核数量 K 一般为 2 的次方倍
- 卷积核的空间尺寸 F
- 步长 S
- 零填充数量 P
- Pooling layer
- 降维,减少参数数量。在卷积层中不对数据做降采样
- 卷积特征往往对应某个局部的特征,通过池化聚合这些局部特征为全局特征
- Max pooling
- 2*2 stride 2
- 避免区域重叠
- Average pooling
06. Training neural networks I
-
Activation functions 激活函数
- 不使用激活函数,最后的输出会是输入的线性组合。利用激活函数对数据进行修正。
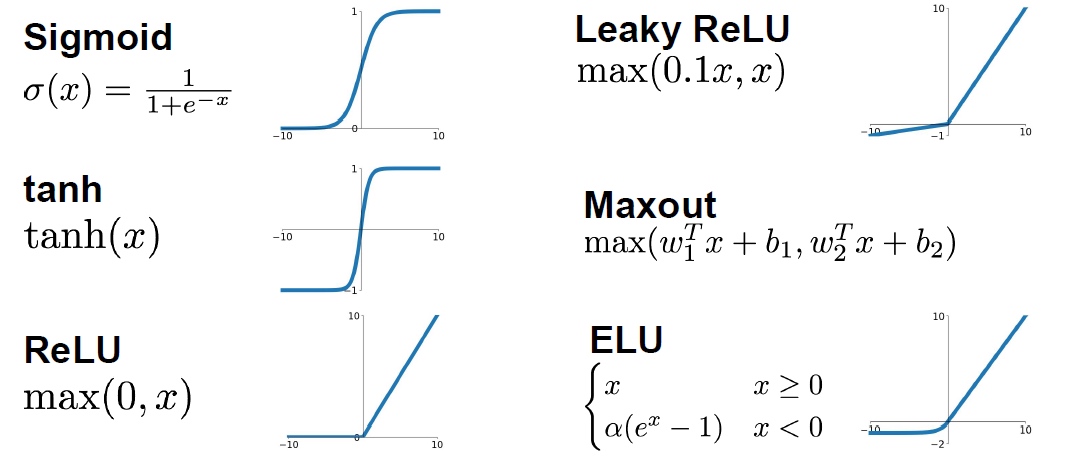
- Sigmoid
- 限制输出在 [0,1]区间内
- firing rate
- 二分类输出层激活函数
- Problem
- 梯度消失:x很大或者很小时,梯度很小,接近于0(考虑图像中的斜率。无法得到梯度反馈。
- 输出不是 0 均值的数据,梯度更新效率低
- exp is a bit compute expensive
- tanh
- 输出范围 [-1, 1]
- 0 均值
- x 很大时,依然没有梯度
- RELU rectified linear unit 线性修正单元
- 一半空间梯度不会饱和,计算速度快,对结果又有精确的计算
- 不是 0 均值
- Leaky RELU
leaky_RELU(x) = max(0.01x, x)- 梯度不会消失
- 需要学习参数
- ELU
- 比 ReLU 好用
- 反激活机制
- Maxout
- maxout(x) = max(w1.Tx + b1, w2.Tx + b2)
- 梯度不会消失
- 增大参数数量
- 激活函数选取经验
- 使用 ReLU ,但要仔细选取学习率
- 尝试使用 Leaky ReLU Maxout ELU
- 使用 tanh 时,不要抱有太大的期望
- 不要使用 sigmoid
-
数据预处理 Data Preprocessing
- 均值减法:对数据中每个独立特征减去平均值,从几何上来看是将数据云的中心都迁移到原点。
- 归一化:将数据中的所有维度都归一化,使数值范围近似相等。但是在图像处理中,像素的数值范围几乎一致,所以不需要额外处理。
1
2X -= np.mean(X, axis = 1)
X /= np.std(X, axis =1)- 图像归一化
- Subtract the mean image AlexNet
- mean image 32,32,3
- Subtract per-channel mean VGGNet
- mean along each channel = 3 numbers
- 如果需要进行均值减法时,均值应该是从训练集中的图片平均值,然后训练集、验证集、测试集中的图像再减去这个平均值。
- Subtract the mean image AlexNet
- Weight Initialization
- 全零初始化
- 网络中的每个神经元都计算出相同的输出,然后它们就会在反向传播中计算出相同的梯度。神经元之间会从源头上对称。
- Small random numbers
- 初始化权值要非常接近 0 又不能等于 0。将权重初始化为很小的数值,以此来打破对称性
- randn 函数是基于零均值和标准差的高斯分布的随机函数
- W = 0.01 * np.random.rand(D,H)
- 问题:一个神经网络的层中的权重值很小,那么在反向传播的时候就会计算出非常小的梯度。会减小反向传播中的“梯度信号”,在深度网络中就会出现问题。
- Xavier initialization
- W = np.random.rand(in, out) / np.sqrt(in)
- 校准方差,解决输入数据量增长,随机初始化的神经元输出数据的分布中的方差也增大问题。
- He initialization
- W = np.random.rand(in, out) / np.sqrt(in/2)
- 全零初始化
- Batch normalization
- 保证输入到神经网络中的数据服从标准的高斯分布
- 通过批量归一化可以加快训练的速度
- 步骤
- 首先计算每个特征的平均值和平方差
- 通过减去平局值和除以方差对数据进行归一化
Result = gamma * normalizedX + beta- 对数据进行线性变换,相当于对数据分布进行一次移动,可以恢复数据之前的分布特征
- BN 的好处
- 加快训练速度
- 可以使用更快的而学习率
- 减少数据对初始化权值的敏感程度
- 相当于进行一次正则化
- BN 适用于卷积神经网络和常规的 DNN,在 RNN 和增强学习中表现不是很好
- Babysitting the Learning Provess
- Hyperparameter Optimization
- Cross-validation 策略训练
- 小范围内随机搜索
07. Training neural networks II
- Optimization Algorithms:
-
SGD 的问题
x += - learning_rate * dx- 梯度在某一个方向下降速度快,在其他方向下降缓慢
- 遇到局部最小值点,鞍点
-
mini-batches GD
- Shuffling and Partitioning are the two steps required to build mini-batches
- Powers of two are often chosen to be the mini-batch size, e.g., 16, 32, 64, 128.
-
SGD + Momentun
- 动量更新:从物理学角度启发最优化问题
V[t+1] = rho * v[t] + dx; x[t+1] = x[t] - learningRate * V[t+1]- rho 被看做是动量,其物理意义与摩擦系数想类似,常取 0.9 或0.99
- 和 momentun 项更新方向相同的可以快速更新。
- 在 dx 中改变梯度方向后, rho 可以减少更新。momentun 能在相关方向加速 SGD,抑制震荡,加快收敛。
-
Nestrov momentum
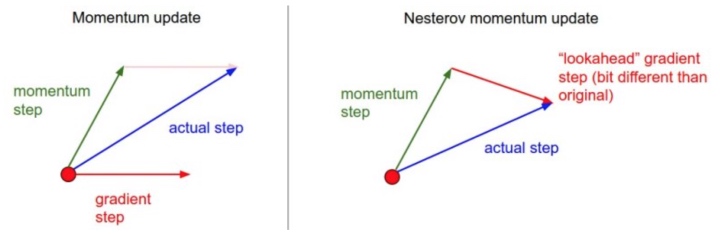
v_prev = v; v = mu * v - learning_rate * dx; x += -mu * v_prev + (1 + mu) * v
-
AdaGrad
- 下面根号中会递推形成一个约束项。前期这一项比较大,能够放大梯度。后期这一项比较小,能约束梯度。
- gt 的平方累积会使梯度趋向于 0
-
RMSProp
- RMS 均方根
- 自适应学习率方法
- 求梯度的平方和平均数:
cache = decay_rate * cache + (1 - decay_rate) * dx**2 x += - learning_rate * dx / (sqrt(cache) + eps)- 依赖全局学习率
-
Adam
- RMSProp + Momentum
- It calculates an exponentially weighted average of past gradients, and stores it in variables (before bias correction) and (with bias correction).
- It calculates an exponentially weighted average of the squares of the past gradients, and stores it in variables (before bias correction) and (with bias correction).
- 一阶到导数累积,二阶导数累积
- It updates parameters in a direction based on combining information from “1” and “2”.
- The update rule is, for :
where:
- t counts the number of steps taken of Adam
- L is the number of layers
- and are hyperparameters that control the two exponentially weighted averages.
- is the learning rate
- is a very small number to avoid dividing by zero
特点:
- 适用于大数据集和高维空间。
- 对不同的参数计算不同的自适应学习率。
-
Learning decay
- 学习率随着训练变化,比如每一轮在前一轮的基础上减少一半。
- 防止学习停止
-
Second order optimization
-
- Regularization
- Dropout
- 每一轮中随机使部分神经元失活,减少模型对神经元的依赖,增强模型的鲁棒性。
- Dropout
- Transfer learning
- CNN 中的人脸识别,可以在大型的模型基础上利用少量的相关图像进行继续训练。
09. CNN architectures
- 研究模型的方法:搞清楚每一层的输入和输出的大小关系。
- LeNet - 5 [1998]
- 60k 参数
- 深度加深,图片大小减少,通道数量增加
- ac: Sigmod/tanh
- AlexNet [2012]
- (227,227,3) (原文错误)
- 60M 参数
- LRN:局部响应归一化,之后很少使用
- VGG - 16 [2015]
- 138 M
- 结构不复杂,相对一致,图像缩小比例和通道增加数量有规律
- ZFNet [2013]
- 在 AlexNet 的基础上修改
CONV1: change from (11 x 11 stride 4) to (7 x 7 stride 2)CONV3,4,5: instead of 384, 384, 256 filters use 512, 1024, 512
- 在 AlexNet 的基础上修改
- VGG [2014]
- 模型中只使用 3*3 conv:与 77 卷积有相同的感受野,而且可以将网络做得更深。比如每一层可以获取到原始图像的范围:第一层 33,第二层 55,第三层 77。
- 前面的卷积层参数量很少,模型中大部分参数属于底部的全连接层。
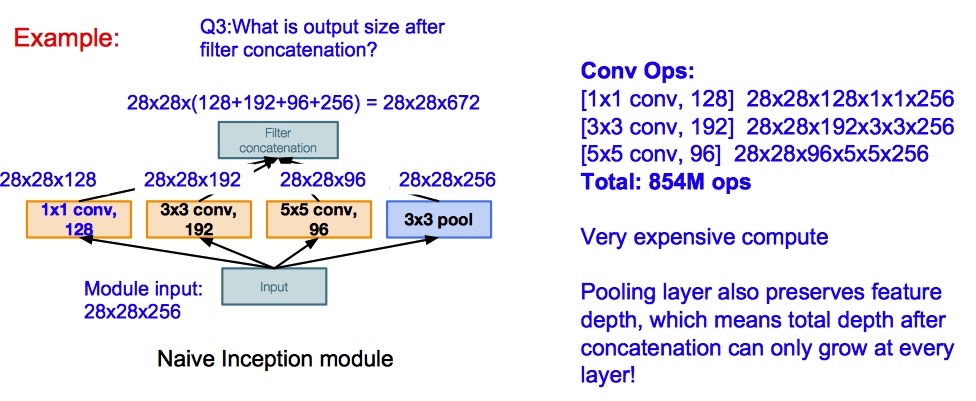
- GoogLeNet
- 引入
Inception module- design a good local network topology (network within a network) and then stack these modules on top of each other
- 该模块可以并行计算
- conv 和 pool 层进行 padding,最后将结果 concat 在一起
- 引入
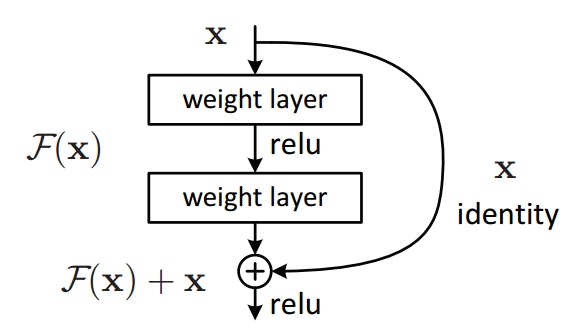
- ResNet
- 目标:深层模型表现不应该差于浅层模型,解决随着网络加深,准确率下降的问题。
Y = (W2* RELU(W1x+b1) + b2) + X- 如果网络已经达到最优,继续加深网络,residual mapping会被设置为 0,一直保存网络最优的情况。
Reference
(WDR) Learning to Estimate the Travel Time
严重申明:本篇文章所有信息从论文、网络等公开渠道中获得,不会透露滴滴地图 ETA 任何实现方法。
这篇论文是滴滴时空数据组 2018 年在 KDD 上发表的关于在 ETA 领域应用深度学习的文章,里面提到模型和技巧大家都应该耳熟能详,最大亮点是工业界的创新。
简单介绍一下背景:ETA 是 Estimate Travel Time 的缩写,中文大概能翻译成到达时间估计。这个问题描述是:在某一个时刻,估计从 A 点到 B 点需要的时间。对于滴滴,关注的是司机开车把乘客从起点送到终点需要的时间。抽象出来 ETA 就是一个时间空间信息相关的回归问题。CTR 中常用的方法都可以在这里面尝试。
对于这个问题:文章首先提到一个最通用的方法 Route ETA:即在获得 A 点到 B 点路线的情况下,计算路线中每一段路的行驶时间,并且预估路口的等待时间。最终 ETA 由全部时间相加得到。这种方法实现起来很简单,也能拿到一些收益。但是仔细思考一下,没有考虑未来道路的通行状态变化情况以及路线的拓扑关系。针对这些问题,文章中提到滴滴内部也有利用 GBDT 或 FM 的方法解决 ETA 问题,不过没有仔细写实现的方法,我也不好继续分析下去。
评价指标
对于 ETA 问题来说,工业界和学术界常用的指标是 MAPE(mean absolute percentage error), 是司机实际从 A 点到 B 点花费的时间, 是 ETA 模型估计出来的时间。得到计算公式如下:
多说一句,如果使用 GBDT 模型实现 ETA 时,这个损失函数的推导有点困难,全网也没有看见几个人推导过。
这个公式主要考虑预估时间偏差大小对用户感知体验的影响,目前我们更加关心极端 badcase 对用户的影响。
特征
- 特征:
- 空间特征:路线序列、道路等级、POI等
- 时间特征:月份、星期、时间片等
- 路况特征:道路的通行速度、拥堵程度
- 个性化信息:司机特征、乘客特征(有「杀熟」风险)、车辆特征
- 附近特征:天气、交通管制
模型
模型包含 3 个部分:
- Wide Learning Models:Wide & Deep 这一部分使用的是 LR + 特征工程,希望模型能记忆一部分的模型。这篇论文中直接利用交叉积学习,减少手动特征工程。
- Deep Neural Networks:对 sparse feature 做一次 Embedding,使用 3 层 MLP 和 ReLU 的网络。
- Long-Short Term Memory:前两部分模块没用使用路线序列特征,所以这部分采用 LSTM 抽取路线特征。由于路线序列是不定长的,论文中的模型是使用最后一个隐藏状态,我们也可以把全部的隐藏状态 reduce_sum 输入到最后的模块。
- Regressor: 将 3 个模型的输出综合起来,作为最后的 ETA 预估。MAPE 作为损失函数,利用 BP 训练模型。

上面模型中使用的特征分类:
- Dense feature:行程级别的实数特征,比如起终点球面距离、起终点 GPS 坐标等。
- Sparse feature:行程级别的离散特征,比如时间片编号、星期几、天气类型等。
- Sequential feature:link 级别的特征,实数特征直接输入模型,而离散特征先做 embedding 再输入模型。注意,这里不再是每个行程一个特征向量,而是行程中每条 link 都有一个特征向量。比如,link 的长度、车道数、功能等级、实时通行速度等。
评估
包括两部分:离线评估和在线评估。
离线评估中取滴滴 2017 年北京前6个月的订单数据,分成两类 pickup (平台给司机分单后,司机开车去接乘客的过程)和 trip (司机接到乘客并前往目的地的过程)。具体数据集划分如下。
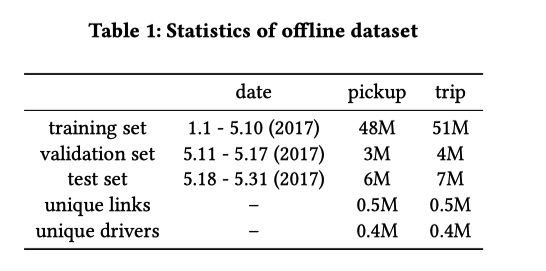
离线使用 MAPE 来评价模型。在线评估时,为了更好的与用户体验挂钩,采用多个指标来衡量 ETA 的效果。包括:
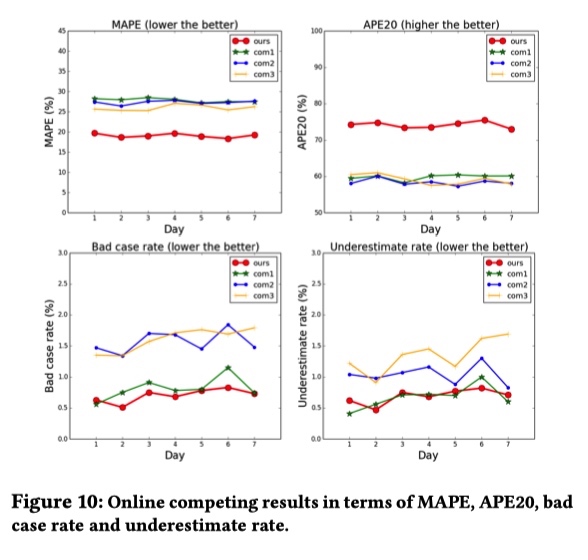
- APE20: absolute percentage error 小于 20% 的订单占比。(越大越好)
- Badcase率:APE 大于 50% 或者 AE 大于 180s 的订单占比,定义为对用户造成巨大影响的情况。(越小越好)
- 低估率:低估订单的比例。(越小越好)
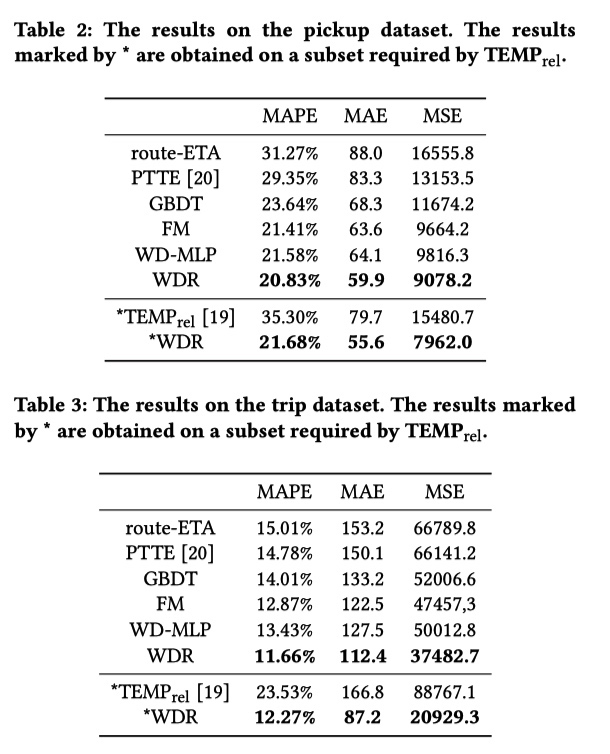
离线结果如下图所示,说来汗颜 PTTE 和 TEMP 是什么算法我都不知道…… WD-MLP 指的是将 WDR 中的 R 部分换成 MLP 。最终 WDR 较 route-ETA 有巨大提升,而且 LSTM 引入的序列信息也在 pikcup 上提升了 0.75%。文章的最后还提出来,LSTM 也可以换成是 Attention,这样替换有什么优点和缺点留给大家思考。
在线实验结果如下图所示,滴滴 ETA MAPE 明显小于 com1、com2、com3 ,这三家地图公司具体是哪三家,大家也能猜到吧。
ETA 服务工程架构
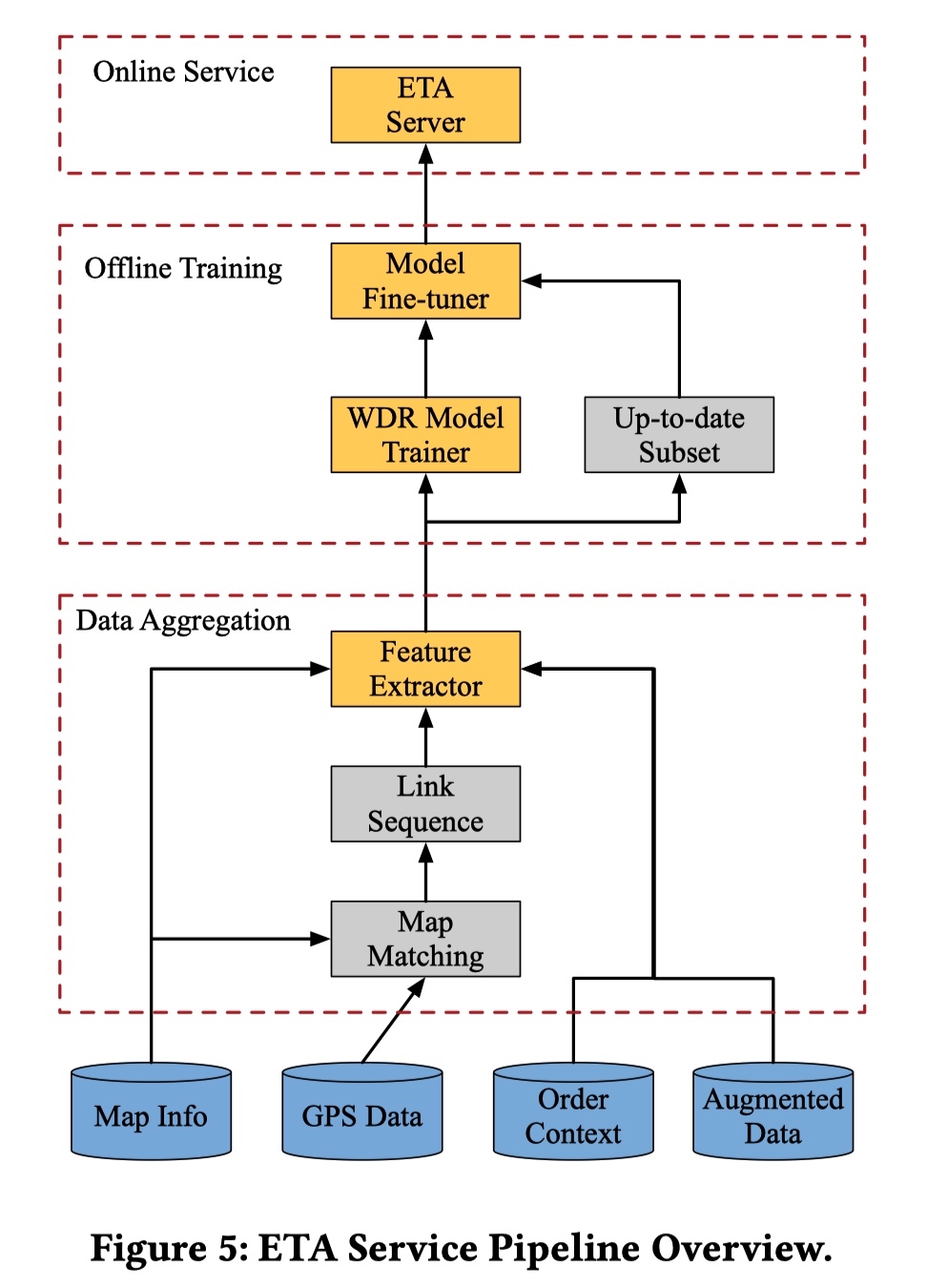
从上面的图中可以看出 ETA 服务工程架构主要包括三个部分:
- Data Aggregation:包括利用 Map Matching 将司机上传到平台的 GPS 对应到滴滴的 Map Info 中得到司机真实行驶过的路线信息,Order Context 指的是订单相关的信息,augmented Data 额外数据比如上文说的交通情况相关信息。
- Offline Training:利用上一步得到的历史数据训练模型。这里可以值得一提的是,ETA 模型是和时间强相关的(节假日和工作日的数据分布明显不同),所以在文章中作者指出将拿出最新的一部分数据用来 fine-tune 训练出来的 WDR 模型。
- Online Service:这里需要一个完整的模型服务系统,其他公司也有很多分享,所以原文没有多提。
FMA-ETA: Estimating Travel Time Entirely Based on FFN With Attention
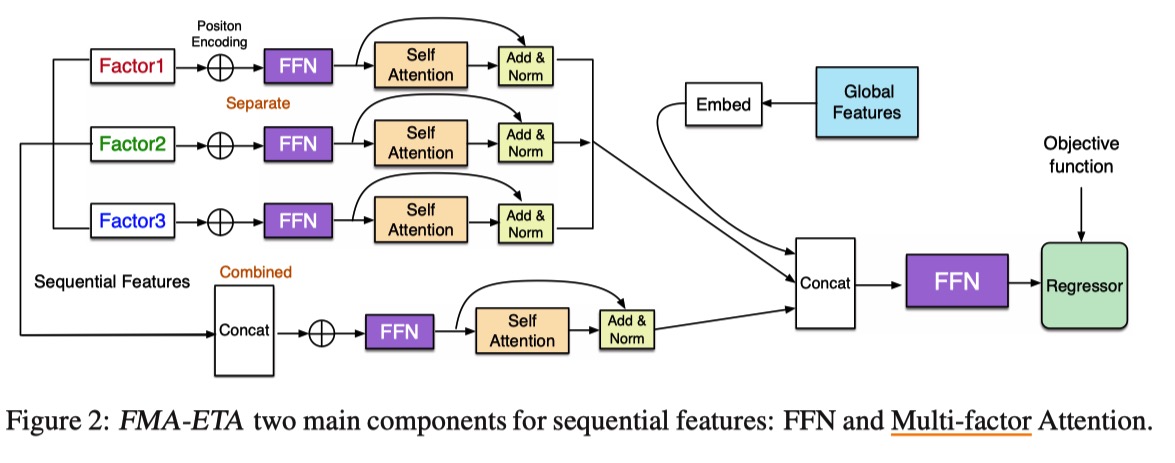
- WDR 模型中 RNN 耗时长,探索基于 Attention 机制的模型
- 对特征分组(multi-factor)去做 Attention 效果比多头要好
- 实验结果分析这部分没有看懂
The deep modules with attention achieve better results than WDR on MAE and RMSE metrics, which means attention mechanism can help to extract features and sole the long-range dependencies in long sequence.
- 遗憾之处
- 新模型预测时延减少,但是没有线上实验结果。
- 暂时没有公开代码和数据集。
总结
从上面简单的介绍来看,ETA 可以使用 CTR 和 NLP 领域的很多技术,大有可为。最后,滴滴 ETA 团队持续招人中(社招、校招、日常实习等),感兴趣者快快和我联系。
说点题外话 你为什么从滴滴出行离职? - 知乎 中提到一点:
8.同年大跃进,在滴滴中高层的眼里,没有BAT。滴滴单量超淘宝指日可待,GAFA才是滴滴要赶超的对象。百度系,LinkedIn系,学院派,uber帮,联想系,MBB就算了,据说连藤校都混成了一个小圈子。。一个项目A team ,B team。一个ETA,投入了多少人力自相残杀?MAPE做到0%又如何?用户体验就爆表了吗?长期留存就高枕无忧了吗?风流总被雨打风吹去,滴滴是二龙山,三虫聚首?是不是正确的事情不知道,反正跟着公司大势所趋,升D10保平安。
参考
Factorization Machines(FM) 由日本 Osaka University 的 Steffen Rendle [1] 在 2010 年提出,是一种常用的因子机模型。
FM
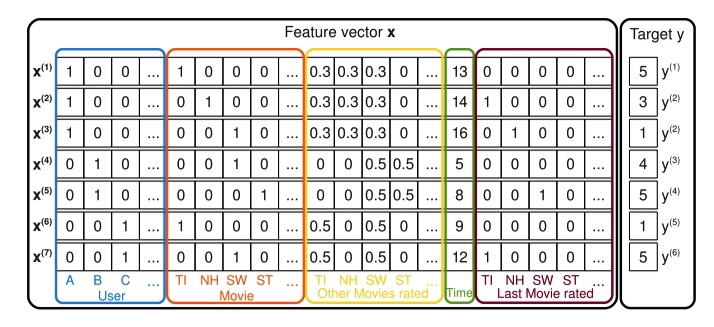
假设现在有一个电影评分的任务,给定如下如所示的特征向量 x(包括用户名、当前在看的电影、已经打分的电影、时间特征、之前看的电影),预测用户对当前观看电影的评分。
作者在线性回归模型的基础上,添加交叉项部分,用来自动组合二阶特征。
其中交叉特征的权重由两个向量的点积得到,可以解决没有在模型中出现的特征组合权重问题,以及减少参数数量。
通过下面的方法来化简交叉项权重计算,算法复杂度降到线性。
对交叉项部分的求导:
其中 与 无关,可以在计算导数前预处理出来。
FM vs SVM
对于经典的特征组合问题,不难想到使用 SVM 求解。Steffen 在论文中也多次将 FM 和 SVM 做对比。
在考虑 SVM 的 Polynomial kernel 为 ,映射
SVM 的公式可以转化为:
论文中提到一句上面的公式中 和 表达能力类似,我猜这也是为什么 FM 中没有自身交叉项的原因吧。
FM 相比于 SVM 有下面三个特点:
- SVM 中虽然也有特征交叉项,但是只能在样本中含有相对应的特征交叉数据时才能学习。但是 FM 能在数据稀疏的时候学习到交叉项的参数。
- SVM 问题无法直接求解,常用的方法是根据拉格朗日对偶性将原始问题转化为对偶问题。
- 在使用模型预测时,SVM 依赖部分训练数据(支持向量),FM 模型则没有这种依赖。
Rank
FM 用来做回归和分类都很好理解,简单写一下如何应用到排序任务中。以 pairwise 为例。假设排序结果有两个文档 和 ,显然用户点击文档有先后顺序,如果先点击 ,记 label ,反之点击 ,label 。模型需要去预测 。
参考逻辑回归,用最大似然对参数进行估计,得到损失函数为 。优化过程和前面提到类似。
NFM
NFM 和 AFM 两篇论文是同一个作者写的,所以文章的结构很相近。
FM 模型由于复杂度问题,一般只使用特征二阶交叉的形式,缺少对 higher-order 以及 non-liner 特征的交叉能力。NFM 尝试通过引入 NN 来解决这个问题。
NFM 的结构如下:第一项和第二项是线性回归,第三项是神经网络。神经网络中利用 FM 模型的二阶特征交叉结果做为输入,学习数据之间的高阶特征。与直接使用高阶 FM 模型相比,可以降低模型的训练复杂度,加快训练速度。
NFM 的神经网络部分包含 4 层,分别是 Embedding Layer、Bi-Interaction Layer、Hidden Layers、Prediction Score。
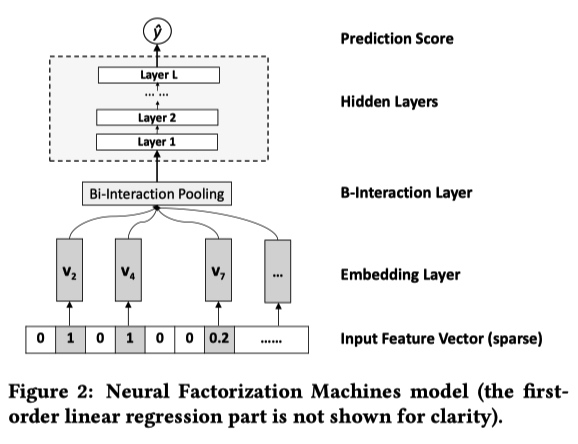
- Embedding Layer 层对输入的稀疏数据进行 Embedding 操作。最常见的 Embedding 操作是在一张权值表中进行 lookup ,论文中作者强调他们这一步会将 Input Feture Vector 中的值与 Embedding 向量相乘。
- Bi-Interaction Layer 层是这篇论文的创新,对 embedding 之后的特征两两之间做 element-wise product,并将结果相加得到一个 k 维(Embeding 大小)向量。这一步相当于对特征的二阶交叉,与 FM 类似,这个公式也能进行化简:
- Hidden Layers 层利用常规的 DNN 学习高阶特征交叉
- Prdiction Layer 层输出最终的结果:
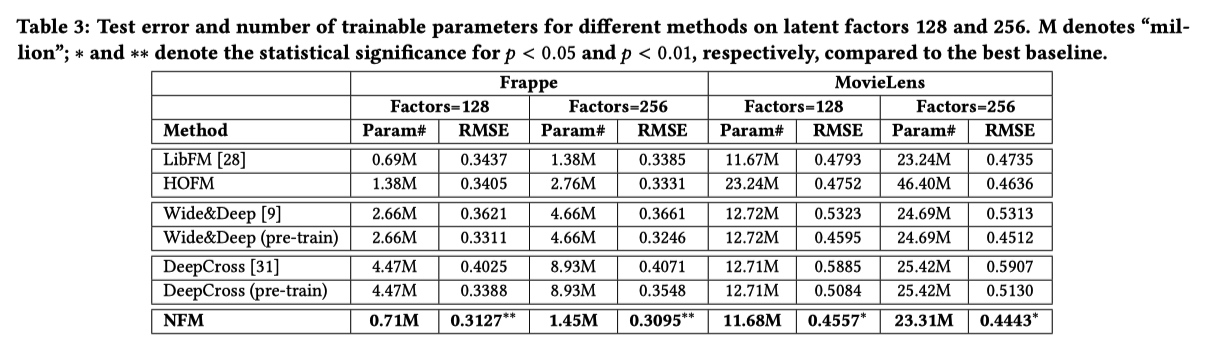
实验结果:
AFM
AFM(Attentional Factorization Machine), 在 FM 的基础上将 Attention 机制引入到交叉项部分,用来区分不同特征组合的权重。
单独看上面公式中的第三项结构:
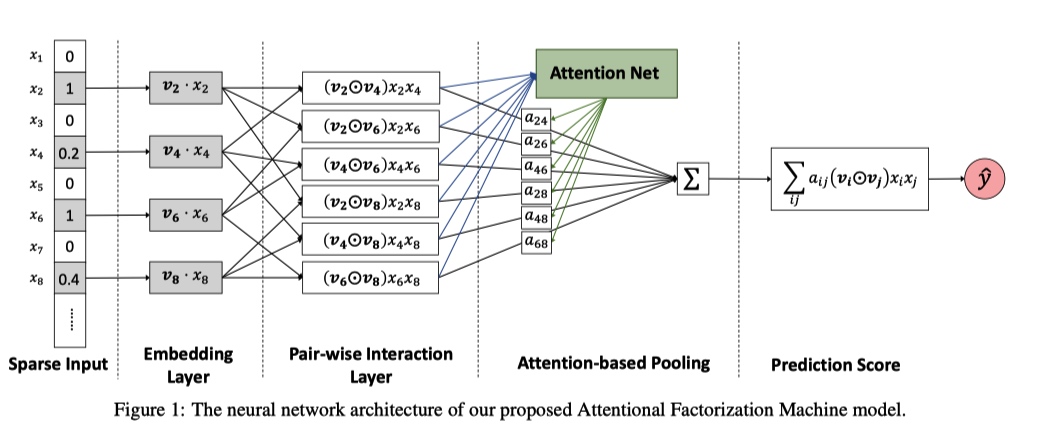
- Embedding Layer 与 NFM 里面的作用一样,转化特征。
- Pair-wise Interaction Layer 是将特征两两交叉,如果对这一步的结果求和就是 FM 中的交叉项。
- Attention 机制在 Attention-based Pooling 层引入。将 Pair-wise Interaction Layer 中的结果输入到 Attention Net 中,得到特征组合的 score ,然后利用 softmax 得到权重矩阵 。
- 最后将 Pair-wise Interaction Layer 中的二阶交叉结果和权重矩阵对应相乘求和得到 AFM 的交叉项。
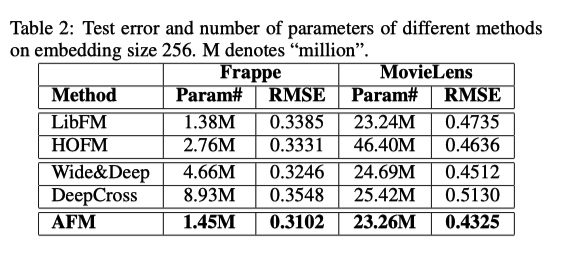
和前一节的实验结果对比,AFM 效果比 NFM 要差一些。这大概就能说明为什么论文中提到 NFM,但是最后没有把 NFM 的结果贴出来,实在是机智。又回到,发论文是需要方法有创新,还是一味追求 state-of-the-art。
参考资料
(Wide&Deep) Wide & Deep Learning for Recommender Systems
背景
这是一篇推荐系统相关的论文,场景是谷歌 Play Store 的 App 推荐。文章开头,作者点明推荐系统需要解决的两个能力: memorization 和 generalization。
memorization 指的是学习数据中出现过的组合特征能力。最常使用的算法是 Logistic Regression,简单、粗暴、可解释性强,而且会人工对特征进行交叉,从而提升效果。但是,对于在训练数据中没有出现过的特征就无能为力。
generalization 指的是通过泛化出现过特征从解释新出现特征的能力。常用的是将高维稀疏的特征转换为低维稠密 embedding 向量,然后使用 fm 或 dnn 等算法。与 LR 相比,减少特征工程的投入,而且对没有出现过的组合有较强的解释能力。但是当遇到的用户有非常小众独特的爱好时(对应输入的数据非常稀疏和高秩),模型会过度推荐。
综合前文 ,作者提出一种新的模型 Wide & Deep。
模型
从文章题目中顾名思义,Wide & Deep 是融合 Wide Models 和 Deep Models 得到,下图形象地展示出来。
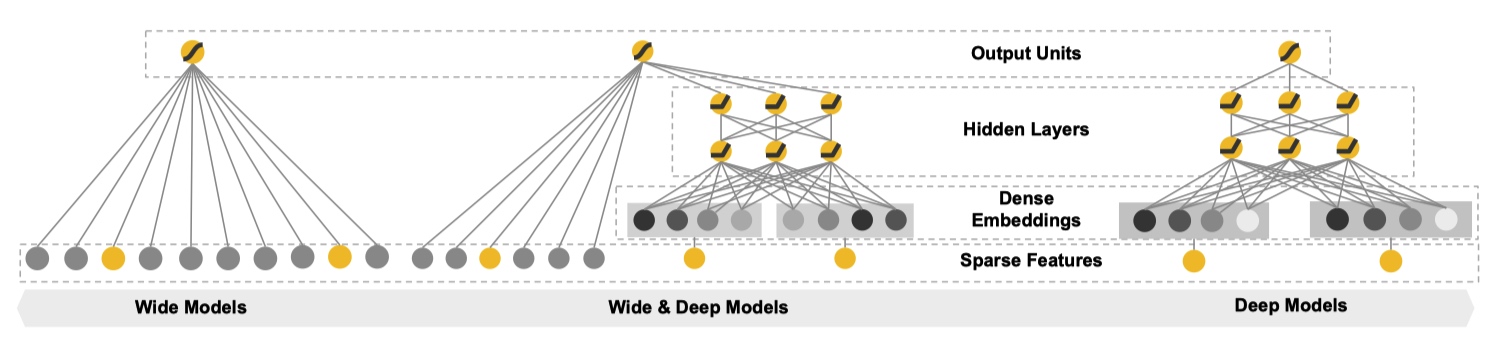
Wide Component 是由一个常见的广义线性模型:。其中输入的特征向量 包括两种类型:原始输入特征(raw input features)和组合特征(transformed features)。
常用的组合特征公式如下:
代表对于第k个组合特征是否包含第i个特征。是布尔变量,代表第i个特征是否出现。例如对于组合特征 AND(gender=female, language=en) 当且仅当 x 满足(“gender=female” and “language=en”)时,。
Deep Component 是一个标准的前馈神经网络,每一个层的形式诸如:。对于输入中的 categorical feature 需要先转化成低维稠密的 embedding 向量,再和其他特征一起喂到神经网络中。
对于这种由基础模型组合得到的新模型,常用的训练形式有两种:joint training 和 ensemble。ensemble 指的是,不同的模型单独训练,且不共享信息(比如梯度)。只有在预测时根据不同模型的结果,得到最终的结果。相反,joint training 将不同的模型结果放在同一个损失函数中进行优化。因此,ensmble 要且模型独立预测时就有有些的表现,一般而言模型会比较大。由于 joint training 训练方式的限制,每个模型需要由不同的侧重。对于 Wide&Deep 模型来说,wide 部分只需要处理 Deep 在低阶组合特征学习的不足,所以可以使用简单的结果,最终完美使用 joint traing。
预测时,会将 Wide 和 Deep 的输出加权得到结果。在训练时,使用 logistic loss function 做为损失函数。模型优化时,利用 mini-batch stochastic optimization 将梯度信息传到 Wide 和 Deep 部分。然后,Wide 部分通过 FTRL + L1 优化,Deep 部分通过 AdaGrad 优化。
实验
本篇论文选择的实验场景是谷歌 app 商店的应用推荐,根据用户相关的历史信息,推荐最有可能会下载的 App。
使用的模型如下:

一些细节:
- 对于出现超过一定次数的 categorical feature,ID 化后放入到模型中。
- Continuous real-valued features 通过 cumulative distribution function 归一化到 [0, 1] 区间。
- categorical feature 由 32 维 embedding 向量组成,最终的输入到 Deep 部分的向量大概在 1200 维。
- 每天在前一天 embedding 和模型的基础上进行增量更新。
实验结果:
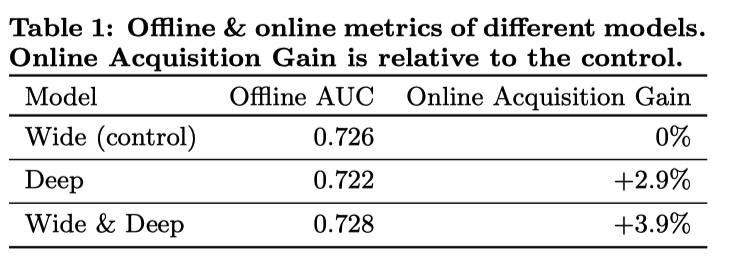
Wide & Deep 模型相对于其他两个模型毫无疑问有提升。但结果中也一个反常的现象:单独使用 Deep 模型离线 AUC 指标比单独使用 Wide 模型差,但是线上对比实验时却有较大的提升。论文中作者用了一句:线下实验中的特征是固定的,线上实验会遇到很多没有出现过的特征组合,Deep 相对于 Wide 有更好的模型泛化能力,所以会有反常现象。由于笔者工作中不关注 AUC,也没有办法继续分析。
总结
作者从推荐系统的的 memorization 和 generalization 入手,设计出新的算法框架。通过线上和线下实验实验,证明 Deep 和 Wide 联合是必须的且有效的。最终也在自己的业务场景带来提升。
Reference
Practical Lessons from Predicting Clicks on Ads at Facebook(gbdt + lr)
**主题:**Facebook 2014 年发表的广告点击预测文章。最主要是提出经典 GBDT+LR 模型,可以自动实现特征工程,效果好比于人肉搜索。另外,文章中还给出一个 online learning 的工程框架。
问题:
- GBDT 如何处理大量 id 类特征
- 广告类对于 user id 的处理:利用出现的频率以及转化率来代替
- id 特征放在 lr 中处理。
- GBDT+LR 和 RF+LR 的区别
- 选出能明显区分正负样本的特征的变换方式,转换成 one hot 有意义
- RF + LR 可以并行训练,但是 RF 中得到的区分度不高
收获:
- 数据支撑去做决策,收获和实验数量成正比。
- CTR click through rate,点击率
- 评价指标:
- Normalized Entropy:越小模型越好
- Calibration:预测点击数除以真实点击数
- AUC 正样本出现在负样本前面的概率。
- 数据新鲜度:模型天级训练比周级训练在 NE 下降 1%。
- GBDT 和 LR 模型采用不同的更新频率,解决训练耗时不同。但是 GBDT 重新训练之后,LR 必须要重新训练。
网络:
GBDT + LR
利用 GBDT 模型进行自动特征组合和筛选,然后根据样本落在哪棵树哪个叶子生成一个 feature vector 输入到 LR 模型中。这种方法的有点在于两个模型在训练过程从是独立,不需要进行联合训练。
GBDT 由多棵 CART 树组成,每一个节点按贪心分裂。最终生成的树包含多层,相当于一个特征组合的过程。根据规则,样本一定会落在一个叶子节点上,将这个叶子节点记为1,其他节点设为0,得到一个向量。比如下图中有两棵树,第一棵树有三个叶子节点,第二棵树有两个叶子节点。如果一个样本落在第一棵树的第二个叶子,将它编码成 [0, 1, 0]。在第二棵树落到第一个叶子,编码成 [1, 0]。所以,输入到 LR 模型中的向量就是 [0, 1, 0, 1, 0]
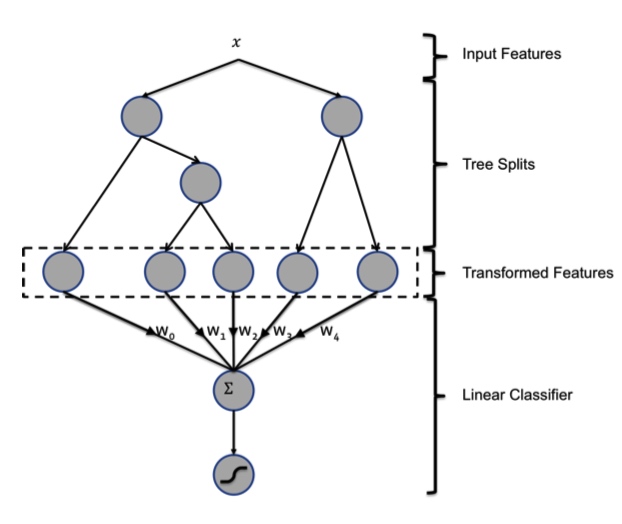
Online Learning
文章中提到的 Online Learning 包括三个部分:
- Joiner 将每次广告展示结果(特征)是否用户点击(标签) join 在一起形成一个完成的训练数据;
- Trainer 定时根据一个 small batch 的数据训练一个模型;
- Ranker 利用上一个模块得到模型预测用户点击。
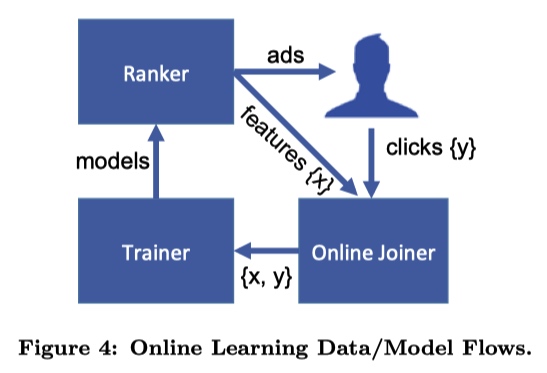
注意的点:
- waiting window time:给用户展示广告之后,我们只能知道用户点击的广告,也就是模型中的正样本。负样本需要设置一个等待时间来判断,即超过某一个时间没有观测到用户点击某一个广告,就认为这是一个负样本。另外设置这个时间也是一个技术活,时间过短导致click没有及时join到样本上,时间太长数据实时性差以及有存储的压力。最后,无论如何都会有一些数据缺失,为了避免累积误差,需要定期重新训练整个模型。
- request ID:人家的模型是分布式架构的,需要使用 request ID 来匹配每次展示给用户的结果以及click。为了实现快速匹配,使用 HashQueue 来保存结果。
- 监控:避免发生意向不到的结果,导致业务损失。我们的实时模型也在上线前空跑了好久。
实验:
有无 GBDT 特征对比
训练两个 LR 模型,一个模型输入样本经过 GBDT 得到的特征,另外一个不输入。混合模型比单独 LR 或 Tree

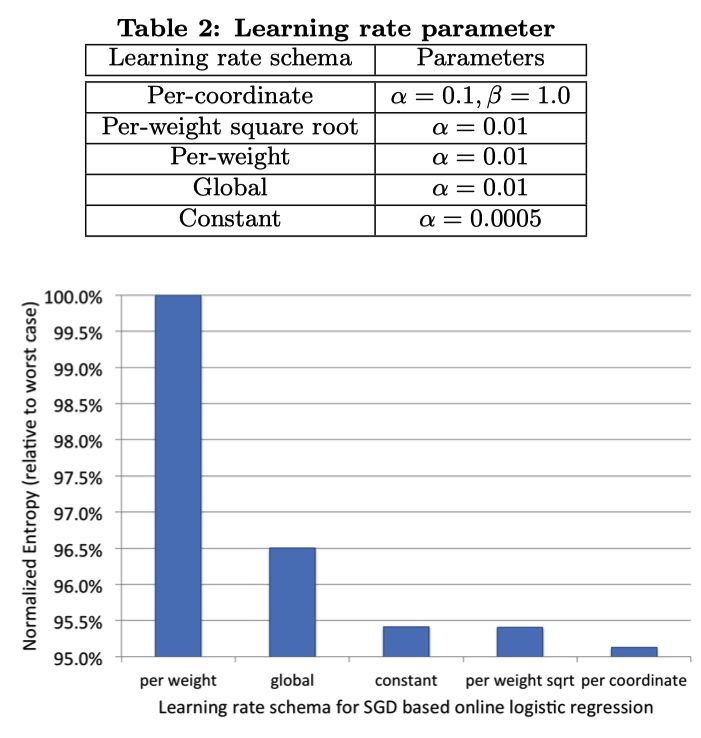
学习率选择
5 种学习率,前三个每一个特征设置一个学习率,最后两种全局学习率。

结果:应该给每一个特征设置一个不同的学习率,而且学习率应该随着轮次缓慢衰减。
GBDT 参数相关实验
- 前面的树会带来大量的收益,但是树越多训练越慢。
- 特征重要程度,累加不同树上某个特征的得分减少贡献。
- 两种特征:
- 上下文,冷启动的时候比较重要,与数据新鲜度有关。
- 历史史特征,权重比较大,关键在于长时间积累。
采样
训练数据大多,需要进行采样。
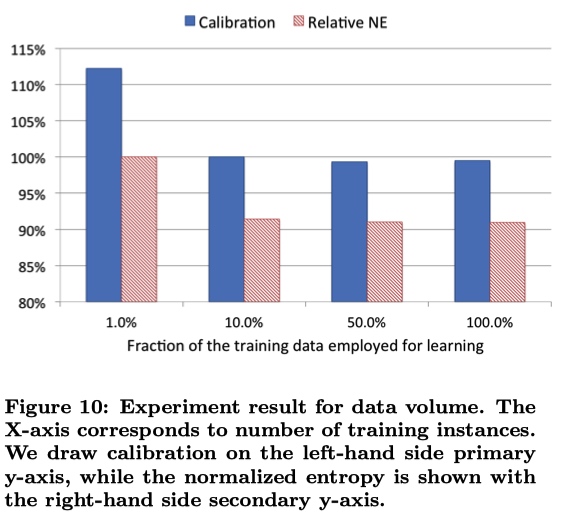
-
uniform subsampling :无差别采样。使用 10 % 的样本,NE 减少 1 %
-
negative down subsampling :对负样本进行下采样。但不是负采样率越低越好,比如下面的图中0.0250就可能是解决了正负样本不平衡问题。最后的CTR指标结果需要重新进行一次映射。
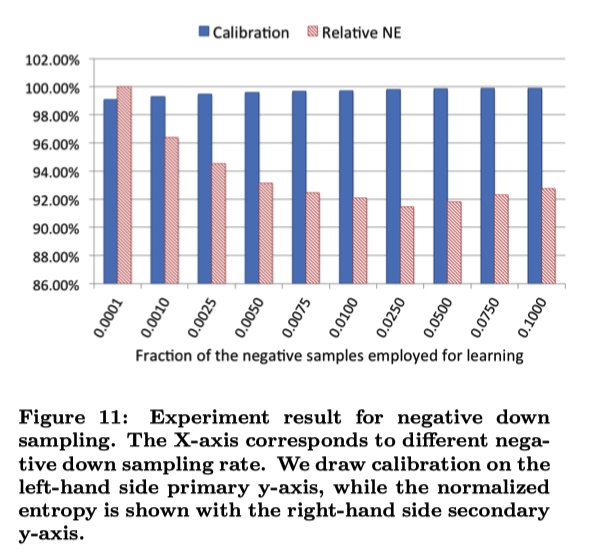
Reference
ImageNet Classification with Deep Convolutional Neural Networks(AlexNet)
作者以及相关性
- Alex Krizhevsky
- Ilya Sutskever
- Geoffrey E. Hinton
- 本文被认为是这一轮深度学习浪潮的开端
主题
- 将 CNN 技术最先应用到图像识别领域,利用 CNN 参数共享的特性,减少网络的规模
- 解决深度网络难训练(速度慢)以及容易过拟合问题(更多数据或者网络技巧)
数据集与指标
- ImageNet LSVRC-2010 contest: 图片 1000 分类
- top-1 和 top-5 错误率为指标
模型/实验/结论
模型
-
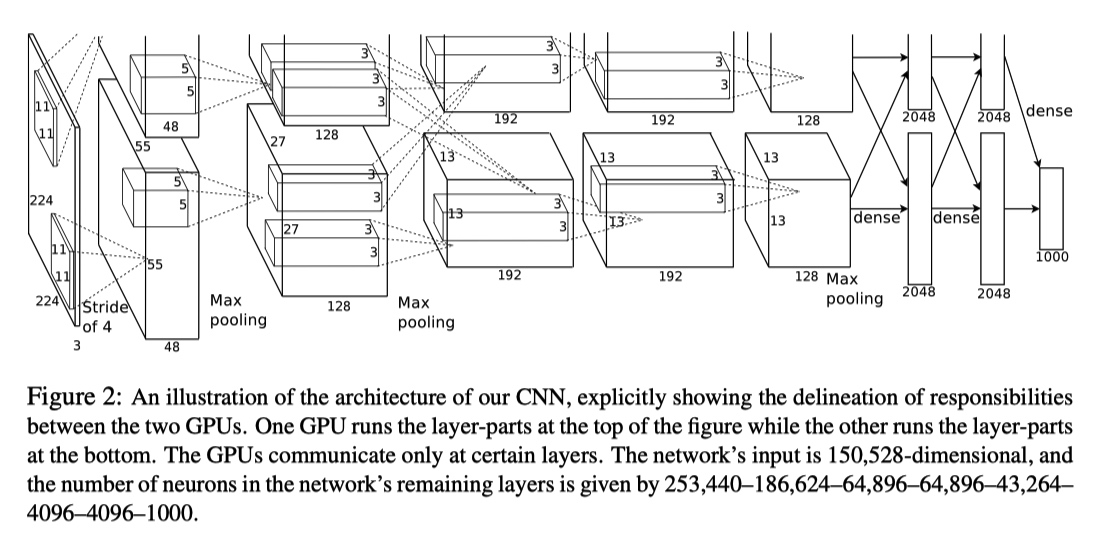
由于当时的 GPU 显存限制,无法将所有的数据加载到单独 GPU 中,作者使用两个 GPU 并行训练。
-
整个模型如下图所示,由 5 个卷积层以及 3 个全连接层组成。其中在 CONV3、FC1、FC2、FC3 层进行两个 GPU 的数据交互。
- [227, 227, 3] INPUT: 原始论文中 224 为笔误。
- [55, 55, 96] CONV1: (11*11*3,96) filters, Stride 4, pad 0
- [27, 27, 96] MAX POOL1: (3*3) filters, Stride 2
- [27, 27, 96] NORM1: Normalization layer
- [27, 27, 256] CONV2: (5*5,256) filters, Stride 1, pad 2
- [13, 13, 256] MAX POOL2: (3*3) filters, Stride 2
- [13, 13, 256] NORM2: Normalization layer
- [13, 13, 384] CONV3: (3*3,384) filters, Stride 1, pad 1
- [13, 13, 384] CONV4: (3*3,384) filters, Stride 1, pad 1
- [13, 13, 384] CONV5: (3*3,256) filters, Stride 1, pad 1
- [6, 6, 256] MAX POOL3: (3*3) filters, Stride 2
- [4096] FC1: 两个 GPU 中的 CONV 层结果进行全连接
- [4096] FC2: FC1 进行全连接
- [1000] FC3: FC2 进行全连接,最后输出分类结果
-
参数数量 60 million
- 使用 ReLU 作为激活函数:比 tanh 计算开销小,以及收敛速度快。根据问题的特点选择激活函数(大模型、大数据集)
- Local Response Normalization(Norm Layers):局部响应归一化层,后来很少使用。
在经过 ReLU 作用之后,对相同空间位置上()的相邻深度( )的卷积结果做归一化。n 指定相邻卷积核数目,N 为该层所有卷积的数目。 都是超参数。本文使用 , 分别降低 top-1 和 top-5 错误 1.4% 和 1.2%
- Pooling:s=2 < z=3,有部分重叠,作者通过实验发现这种方法可以更好地避免过拟合。
- data augmentation:
- 对图像进行裁剪以及翻转,扩大数据。这种策略对测试带来影响,测试时裁剪出图片四个角落以及中间部分,得到 5 张图片,另外翻转得到 5 张图片,最后分类结果又这 10 图片的平均得分确定。
- 利用 PCA 改变 RGB 通道的强度。
- Dropout:每次训练的时候,从模型中 sample 出一个小的模型,减少过拟合。
实验
-
参数:dropout 0.5,batch size 128, SGD Momentum 0.9, Learning rate 1e-2 reduce by 10,L2 weight decay 5e-4
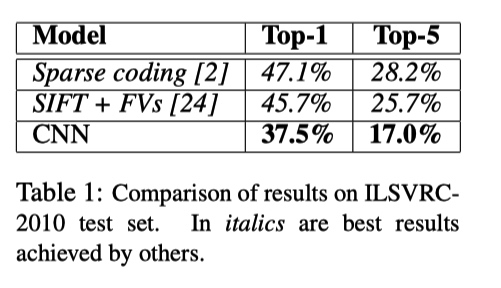
-
测试集上结果
-
取出 CONV1 相关的 filters卷积侧重点不同,GPU1 颜色无关,GPU2 颜色相关。多次实验发现都存在这种现象,说明使用多个 GPU 训练是必要的,模型可以捕捉更多信息。

-
取所有最后一个隐层向量,找到与测试图片欧拉距离最小的训练图片(下图中第一列为测试图片,之后几列是欧拉距离最小的训练集中图片)。肉眼可以发现,同一分类的图片有很大关联性。证明模型能学习图片之间的关系。

结论
- 通过移除 AlexNet 网络中的某几层发现错误率均有提高,这个网络时必要以及有效的。
- 文章中作者通过大量的实验确定模型的细节问题,值得我们学习。
- 当时的 GPU 限制作者的想象力……
西瓜书 周志华 2016 年 12 月第 14 次印刷
3.1 基本形式
线性模型的预测函数为:
写成向量模式得到:
3.2 线性回归
线性回归能在给定数据集 ,其中 学到一个线性模型从而进行预测。
考虑最简单情况,当 为一维时,问题转换为求下式:
使得
使用平方损失函数作为衡量线性规划模型性能的指标, 与 越接近,代表平方损失函数越小。即得到:
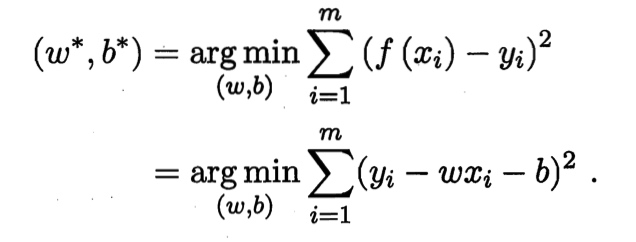
西瓜书 周志华 2016 年 12 月第 14 次印刷
1.1 引言
机器学习:利用经验来决策
1.2 基本术语
根据数据是否拥有标记信息分类:
- 监督学习 supervised learning
- 分类 classification
- 回归 regression
- 无监督学习 unsupervised learning
- 聚类 clustering
1.3 假设空间
假设空间指的是所有跟问题相关的假设所组成的空间,学习过程是从假设空间中进行搜索,目标是找到与训练集「匹配」(fit)的假设。
在这么多的假设中,可能存在一些假设,得出的结果和训练集一致,这些假设组成的空间叫做「版本空间」(version space)。
1.4 归纳偏好
对于数据集中没有出现过的情况,算法可能会按照自己的偏好来预测结果,这种情况称为「归纳偏好」。为算法选取偏好时,可以使用「奥卡姆剃刀」原则,即有多个假设与观察一致,则选最简单的那个。但是什么是最简单的也需要仔细思考。
没有免费的午餐定理(No Free Lunch Theorem, NFL)
- 在所有问题出现的机会相同时,所有的算法的期望性能相同。
- 任何一个算法都有表现好的问题,也有表现差的问题。
- 针对具体的学习问题研究算法。脱离具体问题,研究什么算法更好毫无意义。
1.7 阅读材料
其他科学研究中采用的假设选择原则
古希腊哲学家伊壁鸠鲁 「多释原则」:保留与经验观察一致的原则。