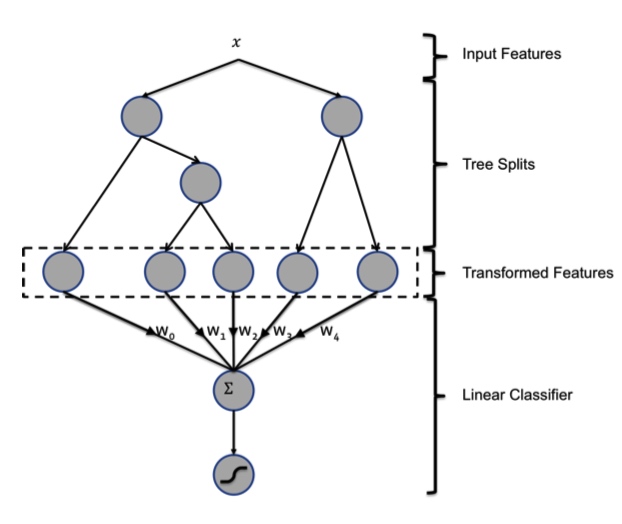
GBDT(Gradient Boosting Decision Tree) 从名字上理解包含三个部分：提升、梯度和树。它最早由 Freidman 在 greedy function approximation ：a gradient boosting machine 中提出。很多公司线上模型是基于 GBDT+FM 开发的，我们 Leader 甚至认为 GBDT 是传统的机器学习集大成者。断断续续使用 GBDT 一年多后，大胆写一篇有关的文章和大家分享。

朴素的想法

假设有一个游戏：给定数据集 ${(x_1,y_1),(x_2,y_2),...,(x_n,y_n)}$，寻找一个模型${\hat y=F(x_i)}$，使得平方损失函数 ${\sum \frac{1}{2}(\hat y_i - y_i)^2}$ 最小。

如果你的朋友提供一个可以使用但是不完美的模型，比如

$$F(x_1)=0.8,y_1=0.9$$

$$F(x_2)=1.4,y_2=1.3$$

在如何不修改这个模型的参数情况下，提高模型效果？

一个简单的思路是：重新训练一个模型实现

$$F(x_1)+h(x_1)=y_1$$

$$F(x_2)+h(x_2)=y_2$$

$$...$$

$$F(x_n)+h(x_n)=y_n$$

换一个角度是用模型学习数据 ${(x_1,y_1-F(x_1)),(x_2,y_2-F(x_2)),...,(x_n,y_n-F(x_n))}$。得到新的模型 ${\hat y=F(x_i)+h(x_i)}$。

其中 ${y_i-F(x_i)}$ 的部分被我们称之为残差，即之前的模型没有学习到的部分。重新训练模型 ${h(x)}$正是学习残差。如果多次执行上面的步骤，可以将流程描述成：

$${F_0(x)}$$

$${F_1(x)=F_0(x)+h_1(x)}$$

$${F_2(x)=F_1(x)+h_2(x)}$$

$${...}$$

$${F_t(x)=F_t-1(x)+h_t(x)}$$

即 ${F(x;w)=\sum^T_{t=1}h_t(x;w)}$，这也就是 GBDT 。

如何理解 Gradient Boosting Decision Tree ?

Gradient Boosting Decision Tree 简称 GBDT，最早由 Friedman 在论文《Greedy function approximation: a gradient boosting machine》中提出。简单从题目中理解包含三个部分内容：Gradient Descent、Boosting、Decision Tree。

Decision Tree 即决策树，利用超平面对特征空间划分来预测和分类，根据处理的任务不同分成两种：分类树和回归树。在 GBDT 算法中，用到的是 CART 即分类回归树。用数学语言来描述为 ${F=\{f(x)=w_{q(x)}\}}$，完成样本 ${x}$ 到决策树叶子节点 ${q(x)}$ 的映射，并将该叶子节点的权重 ${w_{q(x)}}$ 赋给样本。CART 中每次通过计算 gain 值贪心来进行二分裂。

Boosting 是一种常用的集成学习方法（另外一种是 Bagging）。利用弱学习算法，反复学习，得到一系列弱分类器（留一个问题，为什么不用线性回归做为弱分类器）。然后组合这些弱分类器，构成一个强分类器。上面提到的模型 ${F(x;w)=\sum^T_{t=1}h_t(x)}$ 即是一种 boosting 思路，依次训练多个 CART 树 ${h_i}$，并通过累加这些树得到一个强分类器 ${F(x;w)}$。

为什么 GBDT 可行？

在 2 中我提到 GBDT 包括三个部分并且讲述了 Boosting 和 Decison Tree。唯独没有提到 Gradient Descent，GBDT 的理论依据却恰恰和它相关。

回忆一下，Gradient Descent 是一种常用的最小化损失函数 ${L(\theta)}$ 的迭代方法。

• 给定初始值 ${\theta_0}$
• 迭代公式：${\theta ^t = \theta ^{t-1} + \Delta \theta}$
• 将 ${L(\theta ^t)}$ 在 ${\theta ^{t-1}}$ 处进行一阶泰勒展开：${L(\theta ^t)=L(\theta ^{t-1} + \Delta \theta) \approx L(\theta ^{t-1}) + L^\prime(\theta ^{t-1})\Delta \theta}$
• 要使 ${L(\theta ^t) < L(\theta ^{t-1}) }$，取 ${\Delta \theta = -\alpha L^\prime(\theta ^{t-1})}$
• 其中 ${\alpha}$ 是步长，可以通过 line search 确定，但一般直接赋一个很小的数。

在 1 中提到的问题中，损失函数是 MSE ${L(y, F(x))=\frac{1}{2}(y_i - f(x_i))^2}$。

我们的任务是通过调整 ${F(x_1), F(x_2), ..., F(x_n)}$ 最小化 ${J=\sum_i L(y_i, F(x_i))}$。

如果将 ${F(x_i)}$ 当成是参数，并对损失函数求导得到 ${ \frac{\partial J}{\partial F(x_i)} = \frac{\partial \sum_i L(y_i, F(x_i))}{\partial F(x_i)} = \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} = F(x_i)-y_i}$。

可以发现，在 1 中提到的模型 ${h(x)}$ 学习的残差 ${y_i-F(x_i)}$正好等于负梯度，即 ${y_i-F(x_i)=-\frac{\partial J}{\partial F(x_i)}}$。

所以，参数的梯度下降和函数的梯度下降原理上是一致的：

• ${F_{t+1}(x_i)=F_t(x_i)+h(x_i)=F(x_i)+y_i-F(x_i)=F_t(x_i)-1\frac{\partial J}{\partial F(x_i)}}$
• ${\theta ^t = \theta ^{t-1} + \alpha L^\prime(\theta ^{t-1})}$

GBDT 算法流程

模型 F 定义为加法模型：

$${F(x;w)=\sum^{M}_{m=1} \alpha_m h_m(x;w_m) = \sum^{M}_{m=1}f_t(x;w_t)}$$

其中，x 为输入样本，h 为分类回归树，w 是分类回归树的参数，${\alpha}$ 是每棵树的权重。

通过最小化损失函数求解最优模型：${F^* = argmin_F \sum^N_{i=1}L(y_i, F(x_i))}$

输入: ${(x_i,y_i),T,L}$

1. 初始化：${f_0(x)}$
2. 对于 ${t = 1 to T}$ ：
   1. 计算负梯度（伪残差）： ${ \tilde{y_i} = -[\frac{\partial L(y_i, F(x_i))}{\partial F(x)}]_{F(x)=F_{m-1}(x)} ,i=1,2,...,N}$
   2. 根据 ${\tilde{y_i}}$ 学习第 m 棵树： ${w^*=argmin_{w} \sum_{i=1}^N(\tilde{y_i} - h_t(x_i;w))^2}$
   3. line searcher 找步长：${\rho^* = argmin_\rho \sum_{i=1}^{N}L(y_i, F_{t-1}(x_i)+\rho h_t(x_i;w^*))}$
   4. 令 ${f_t=\rho^*h_t(x;w*)}$，更新模型：${F_t=F_{t-1}+f_t}$
3. 输出 ${F_T}$

说明：

1. 初始化 ${f_0}$ 方法
   1. 求解损失函数最小
   2. 随机初始化
   3. 训练样本的充分统计量
2. 每一轮拟合负梯度，而不是拟合残差，是为方便之后扩展到其他损失函数。
3. 最小化问题中，如果有解析解，直接带入。否则，利用泰勒二阶展开，Newton Step 得到近似解。

这一篇就先到这里，之后还会分享 GBDT 常用损失函数推导以及 XGboost 相关内容。如果有任何想法，都可以在留言区和我交流。

Reference

1. 李航, 《统计学习方法》8.4 提升树
2. Freidman，greedy function approximation ：a gradient boosting machine
3. 【19年ML思考笔记】GBDT碎碎念（1）谈回归树的分裂准则 - 知乎
4. 机器学习-一文理解GBDT的原理-20171001 - 知乎
5. GBDT入门详解 - Scorpio.Lu|Blog
6. python - Why Gradient Boosting not working in Linear Regression? - Stack Overflow
7. GBDT基本原理及算法描述 - Y学习使我快乐V的博客 - CSDN博客
8. GBDT的那些事儿 - 知乎

**主题：**Facebook 2014 年发表的广告点击预测文章。最主要是提出经典 GBDT+LR 模型，可以自动实现特征工程，效果好比于人肉搜索。另外，文章中还给出一个 online learning 的工程框架。

问题：

• GBDT 如何处理大量 id 类特征
  • 广告类对于 user id 的处理：利用出现的频率以及转化率来代替
  • id 特征放在 lr 中处理。
• GBDT+LR 和 RF+LR 的区别
  • 选出能明显区分正负样本的特征的变换方式，转换成 one hot 有意义
  • RF + LR 可以并行训练，但是 RF 中得到的区分度不高

收获：

• 数据支撑去做决策，收获和实验数量成正比。
• CTR click through rate，点击率
• 评价指标：
  • Normalized Entropy：越小模型越好
  • Calibration：预测点击数除以真实点击数
  • AUC 正样本出现在负样本前面的概率。
• 数据新鲜度：模型天级训练比周级训练在 NE 下降 1%。
• GBDT 和 LR 模型采用不同的更新频率，解决训练耗时不同。但是 GBDT 重新训练之后，LR 必须要重新训练。

网络：

GBDT + LR

利用 GBDT 模型进行自动特征组合和筛选，然后根据样本落在哪棵树哪个叶子生成一个 feature vector 输入到 LR 模型中。这种方法的有点在于两个模型在训练过程从是独立，不需要进行联合训练。

GBDT 由多棵 CART 树组成，每一个节点按贪心分裂。最终生成的树包含多层，相当于一个特征组合的过程。根据规则，样本一定会落在一个叶子节点上，将这个叶子节点记为1，其他节点设为0，得到一个向量。比如下图中有两棵树，第一棵树有三个叶子节点，第二棵树有两个叶子节点。如果一个样本落在第一棵树的第二个叶子，将它编码成 [0, 1, 0]。在第二棵树落到第一个叶子，编码成 [1, 0]。所以，输入到 LR 模型中的向量就是 [0, 1, 0, 1, 0]

Online Learning

文章中提到的 Online Learning 包括三个部分：

• Joiner 将每次广告展示结果（特征）是否用户点击（标签） join 在一起形成一个完成的训练数据；
• Trainer 定时根据一个 small batch 的数据训练一个模型；
• Ranker 利用上一个模块得到模型预测用户点击。

注意的点：

• waiting window time：给用户展示广告之后，我们只能知道用户点击的广告，也就是模型中的正样本。负样本需要设置一个等待时间来判断，即超过某一个时间没有观测到用户点击某一个广告，就认为这是一个负样本。另外设置这个时间也是一个技术活，时间过短导致click没有及时join到样本上，时间太长数据实时性差以及有存储的压力。最后，无论如何都会有一些数据缺失，为了避免累积误差，需要定期重新训练整个模型。
• request ID：人家的模型是分布式架构的，需要使用 request ID 来匹配每次展示给用户的结果以及click。为了实现快速匹配，使用 HashQueue 来保存结果。
• 监控：避免发生意向不到的结果，导致业务损失。我们的实时模型也在上线前空跑了好久。

实验：

有无 GBDT 特征对比

训练两个 LR 模型，一个模型输入样本经过 GBDT 得到的特征，另外一个不输入。混合模型比单独 LR 或 Tree

学习率选择

5 种学习率，前三个每一个特征设置一个学习率，最后两种全局学习率。

结果：应该给每一个特征设置一个不同的学习率，而且学习率应该随着轮次缓慢衰减。

GBDT 参数相关实验

• 前面的树会带来大量的收益，但是树越多训练越慢。
• 特征重要程度，累加不同树上某个特征的得分减少贡献。
• 两种特征：
  • 上下文，冷启动的时候比较重要，与数据新鲜度有关。
  • 历史史特征，权重比较大，关键在于长时间积累。

采样

训练数据大多，需要进行采样。

• uniform subsampling ：无差别采样。使用 10 % 的样本，NE 减少 1 %
  

• negative down subsampling ：对负样本进行下采样。但不是负采样率越低越好，比如下面的图中0.0250就可能是解决了正负样本不平衡问题。最后的CTR指标结果需要重新进行一次映射。
  

Reference

• 回顾Facebook经典CTR预估模型 - 知乎