8d - the building blocks - block types
课程汇总链接: [[@Magical Academic Note Taking]]
8d - the building blocks - block types
课程汇总链接: [[@Magical Academic Note Taking]]
课程链接: [[@Magical Academic Note Taking]]
去年学习这门做的部分笔记,现在分享出来。
笔记格式有些问题,持续整理中。
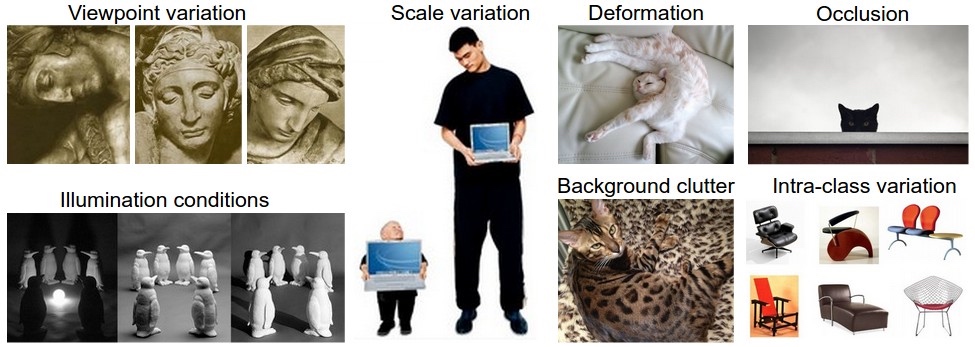

Y = wX + b

R 正则项 $$\lambda$$ 正则化参数
1 | f = np.array([123, 456, 789]) # 例子中有3个分类,每个评分的数值都很大 |
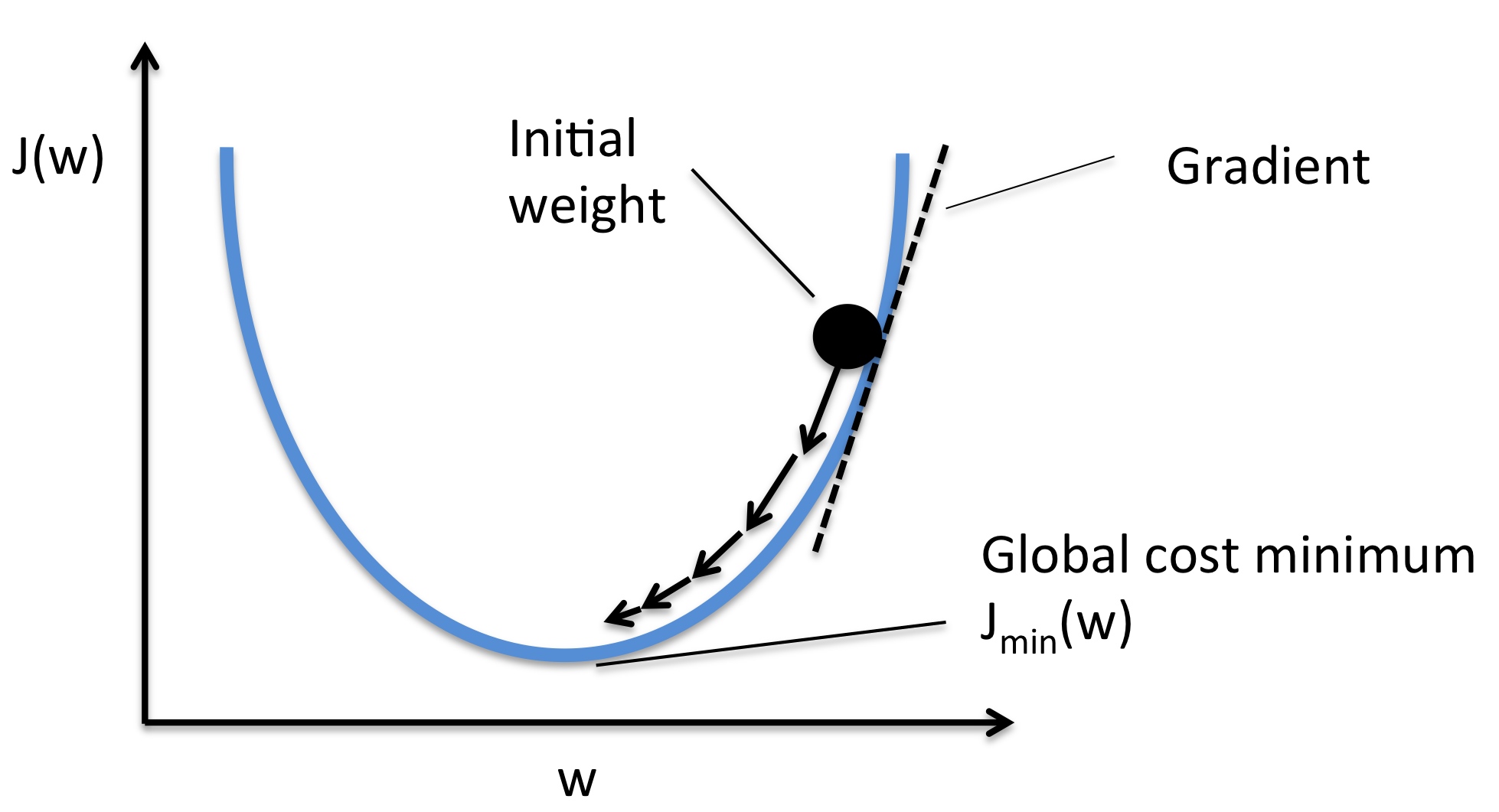
W = W - learning_rate * W_grad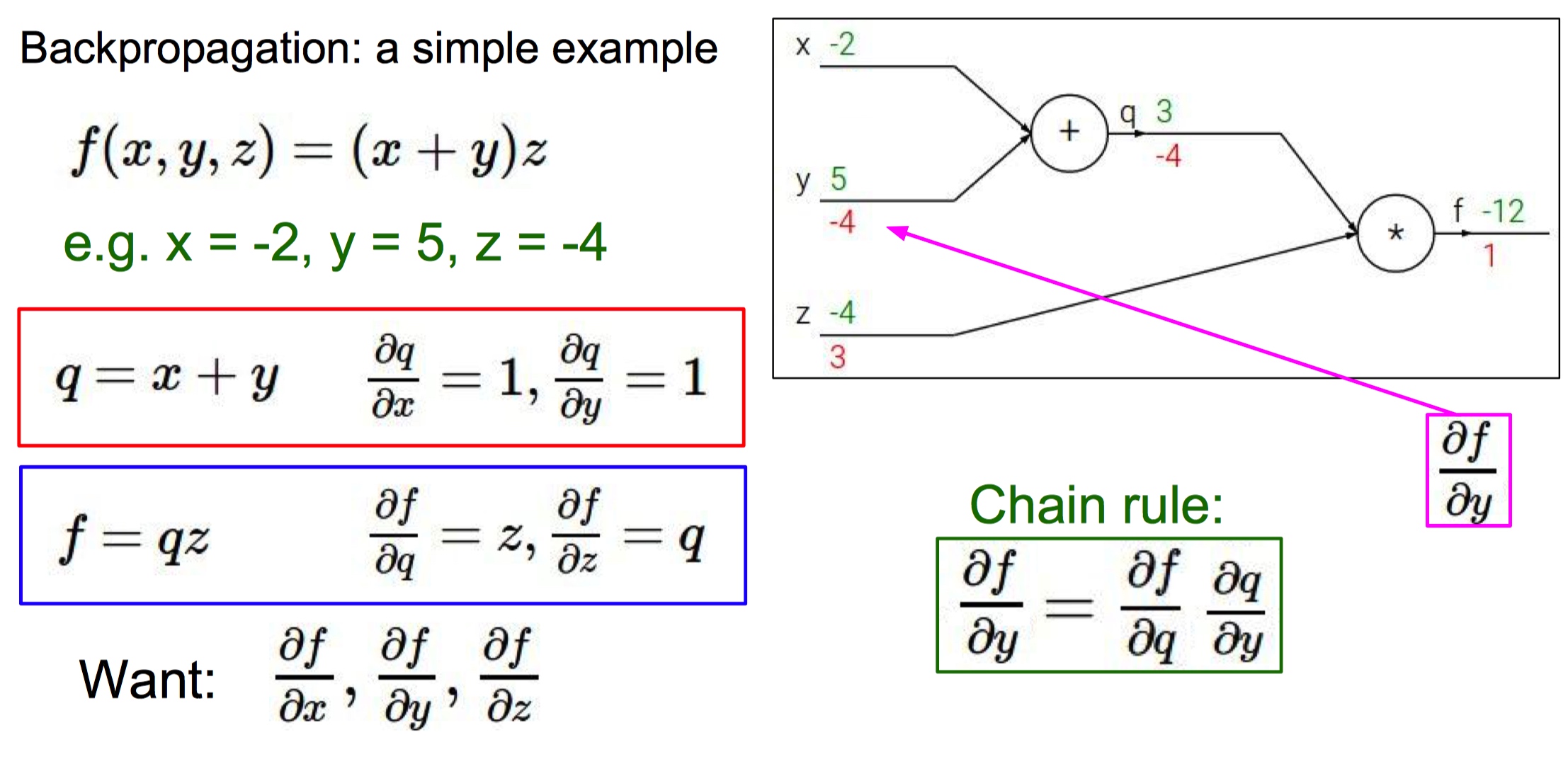
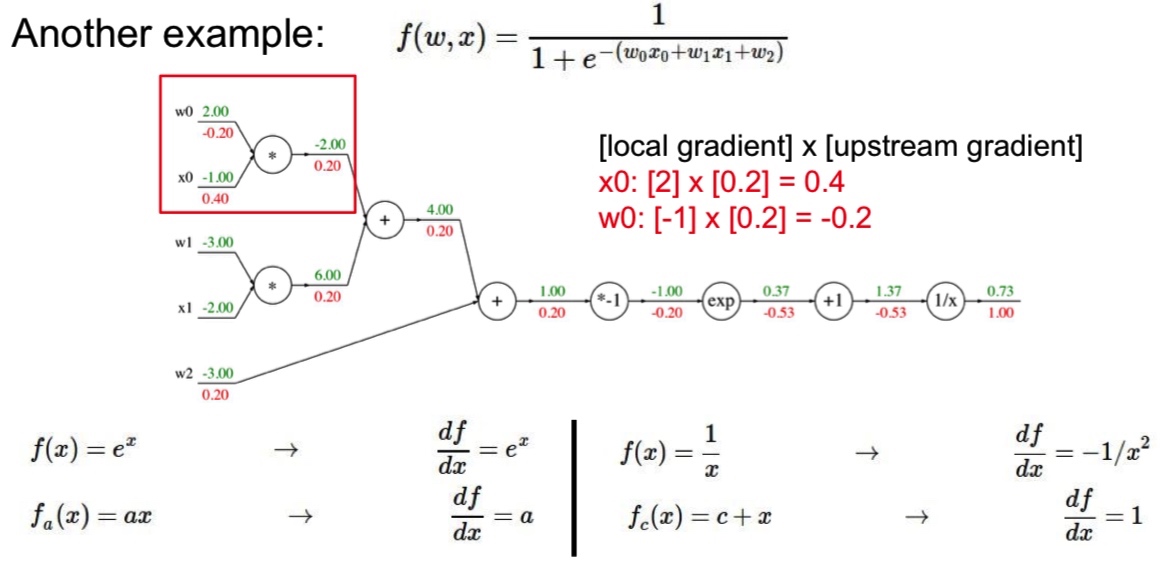
1 | class MultuplyGate(object): |
INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC32*32*3 卷积大小 10 5*5 stride 1 pad 232*32*105*5*3+1 =76 biasActivation functions 激活函数
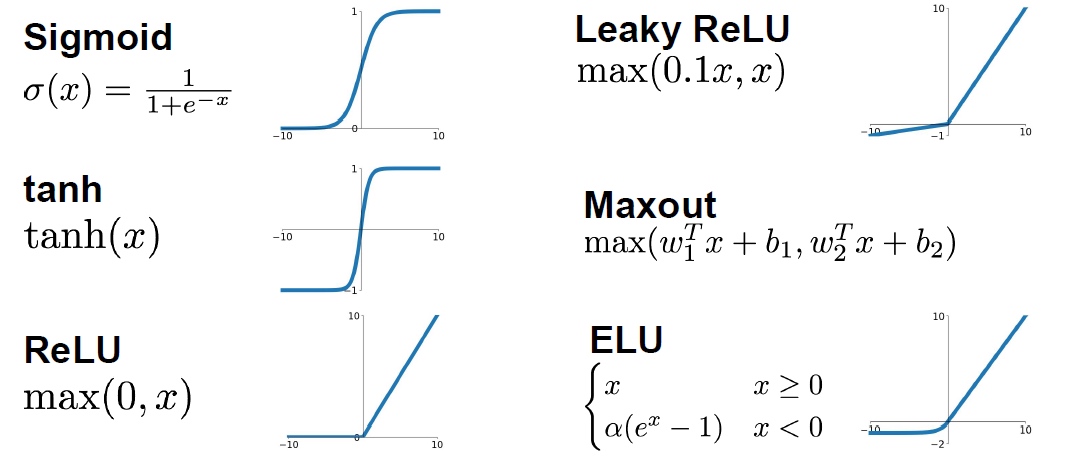
leaky_RELU(x) = max(0.01x, x)数据预处理 Data Preprocessing
1 | X -= np.mean(X, axis = 1) |
Result = gamma * normalizedX + beta
SGD 的问题
x += - learning_rate * dxmini-batches GD
SGD + Momentun
V[t+1] = rho * v[t] + dx; x[t+1] = x[t] - learningRate * V[t+1]Nestrov momentum
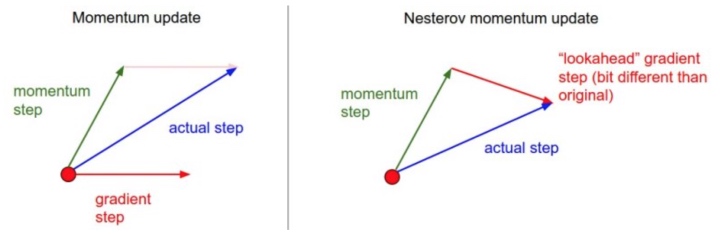
v_prev = v; v = mu * v - learning_rate * dx; x += -mu * v_prev + (1 + mu) * vAdaGrad
RMSProp
cache = decay_rate * cache + (1 - decay_rate) * dx**2x += - learning_rate * dx / (sqrt(cache) + eps)Adam
where:
特点:
Learning decay
Second order optimization
CONV1: change from (11 x 11 stride 4) to (7 x 7 stride 2)CONV3,4,5: instead of 384, 384, 256 filters use 512, 1024, 512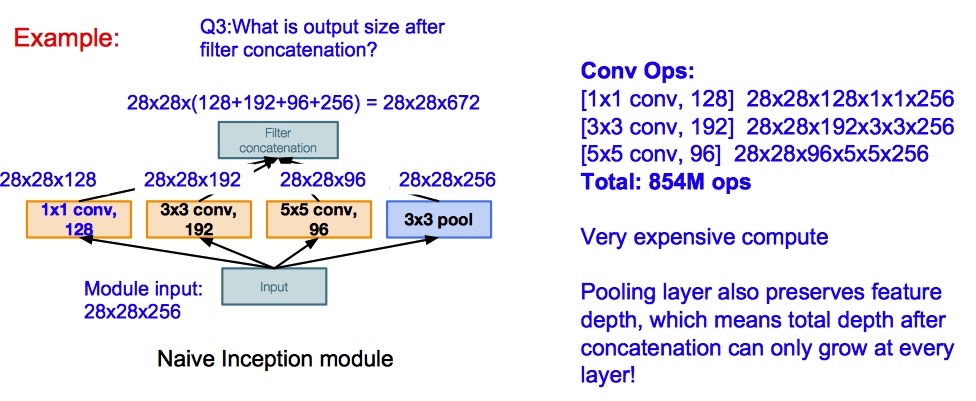
Inception module
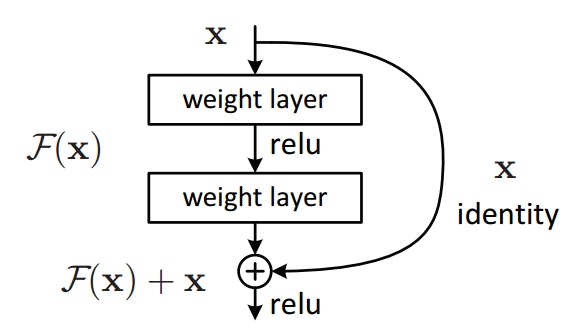
Y = (W2* RELU(W1x+b1) + b2) + X