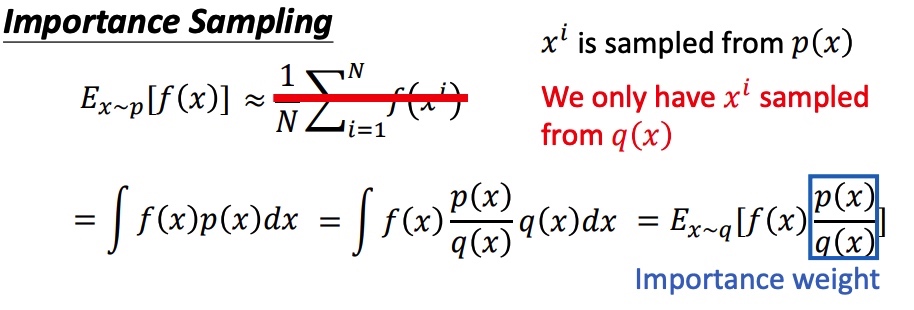Info
课件下载:Hung-yi Lee - Deep Reinforcement Learning
课程视频:DRL Lecture 1: Policy Gradient (Review) - YouTube
- Change Log
- 20191226: 整理 PPO 相关资料
- 20191227: 整理 Q-Learning 相关资料
- 20200906: 拖延半年多没有整理笔记,将剩下的内容整理到单独的笔记中。
我的笔记汇总:
RL 基础
强化学习基本定义:
- Actor:可以感知环境中的状态,通过执行不同的动作得到反馈的奖励,在此基础上进行学习优化。
- Environment:指除 Actor 之外的所有事务,受 Actor 动作影响而改变其状态,并给 Actor 对应的奖励。
- on-policy 和 off-policy 的区别在于 Actor 和 Environment 交互的策略和它自身在学习的策略是否是同一个。
一些符号:
- State s 是对环境的描述,其状态空间是 S。
- Action a 是 Actore 的行为描述,其动作空间是 A。
- Policy π(a∣s)=P[At=a∣St=s] 代表在给定环境状态 s 下 动作 a 的分布。
- Reward r(s,a,s′) 在状态 s 下执行动作 a 后,Env 给出的打分。
Policy Gradient
Policy Network 最后输出的是概率。
目标:调整 actor 中神经网络 policy π(θ),得到 a=π(s,θ),最大化 reward。
trajectory τ 由一系列的状态和动作组成,出现这种组合的概率是 pθ(τ) 。
pθ(τ)=p(s1)pθ(a1∣s1)p(s2∣s1,a1)pθ(a2∣s2)p(s3∣s2,a2)⋯=p(s1)∏l=1Tpθ(at∣st)p(st+1∣st,at)
reward :根据 s 和 a 计算得分 r,求和得到 R。在围棋等部分任务中,无法获得中间的 r(下完完整的一盘棋后能得到输赢的结果)。
需要计算 R 的期望 Rˉθ,形式和 GAN 类似。如果一个动作得到 reward 多,那么就增大这个动作出现的概率。最终达到 agent 所做 policy 的 reward 一直都比较高。
Rˉθ=τ∑R(τ)pθ(τ)
强化学习中,没有 label。需要从环境中采样得到 τ 和 R,根据下面的公式去优化 agent。相当于去求一个 likelihood。
∇f(x)=f(x)f(x)∇f(x)=f(x)∇logf(x) ,这一步中用到对 log 函数进行链式求导。
∇Rˉθ=τ∑R(τ)∇pθ(τ)
=Eτ∼pθ(τ)[R(τ)]logpθ(τ)]≈N1∑n=1NR(τn)∇logpθ(τn)=N1∑n=1N∑t=1TnR(τn)∇logpθ(atn∣stn)
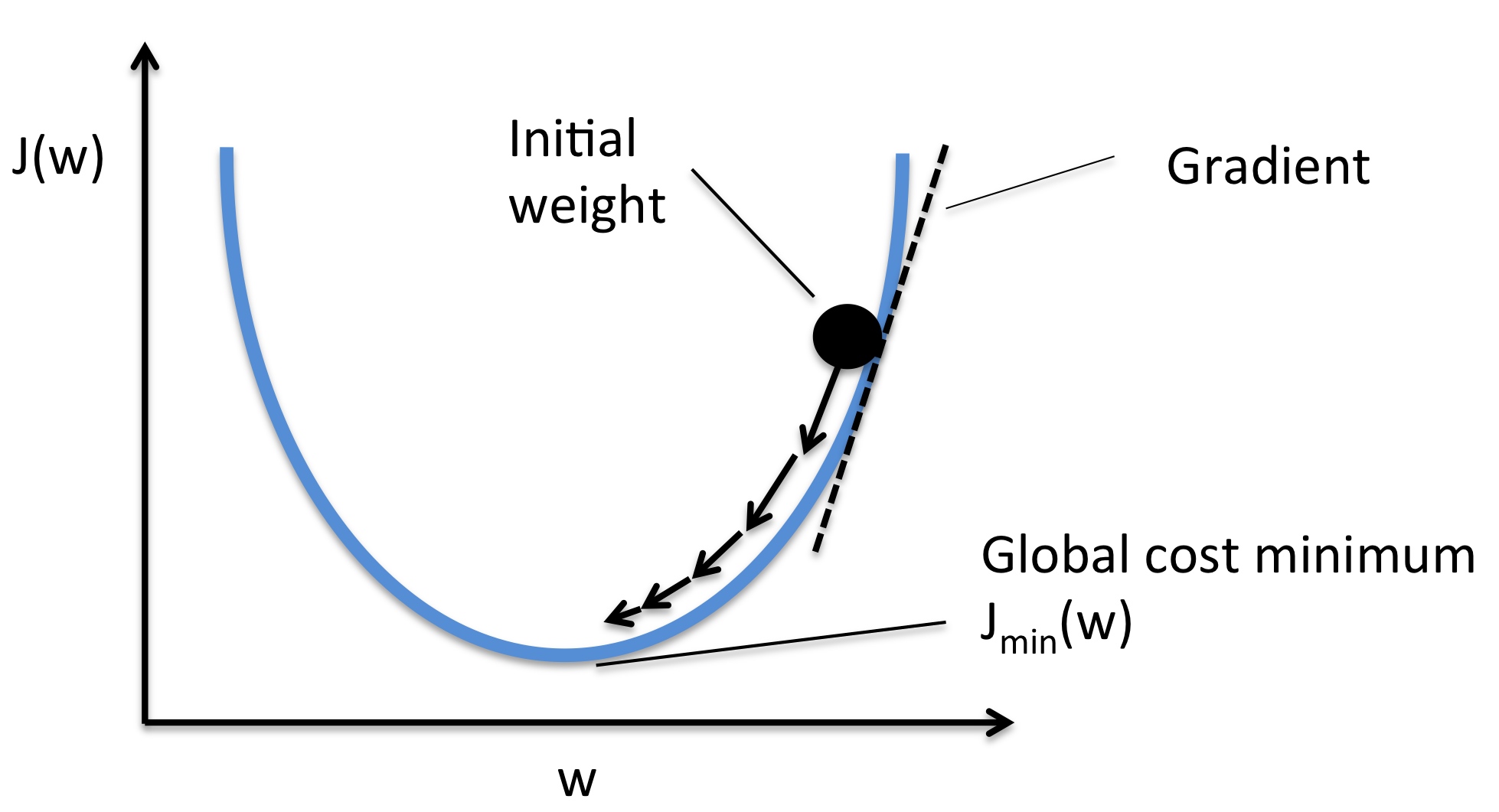
参数更新方法:
- 在环境中进行采样,得到一系列的轨迹和回报。
- 利用状态求梯度,更新模型。如果 R 为正,增大概率 pθ(at∣st), 否则减少概率。
- 重复上面的流程。

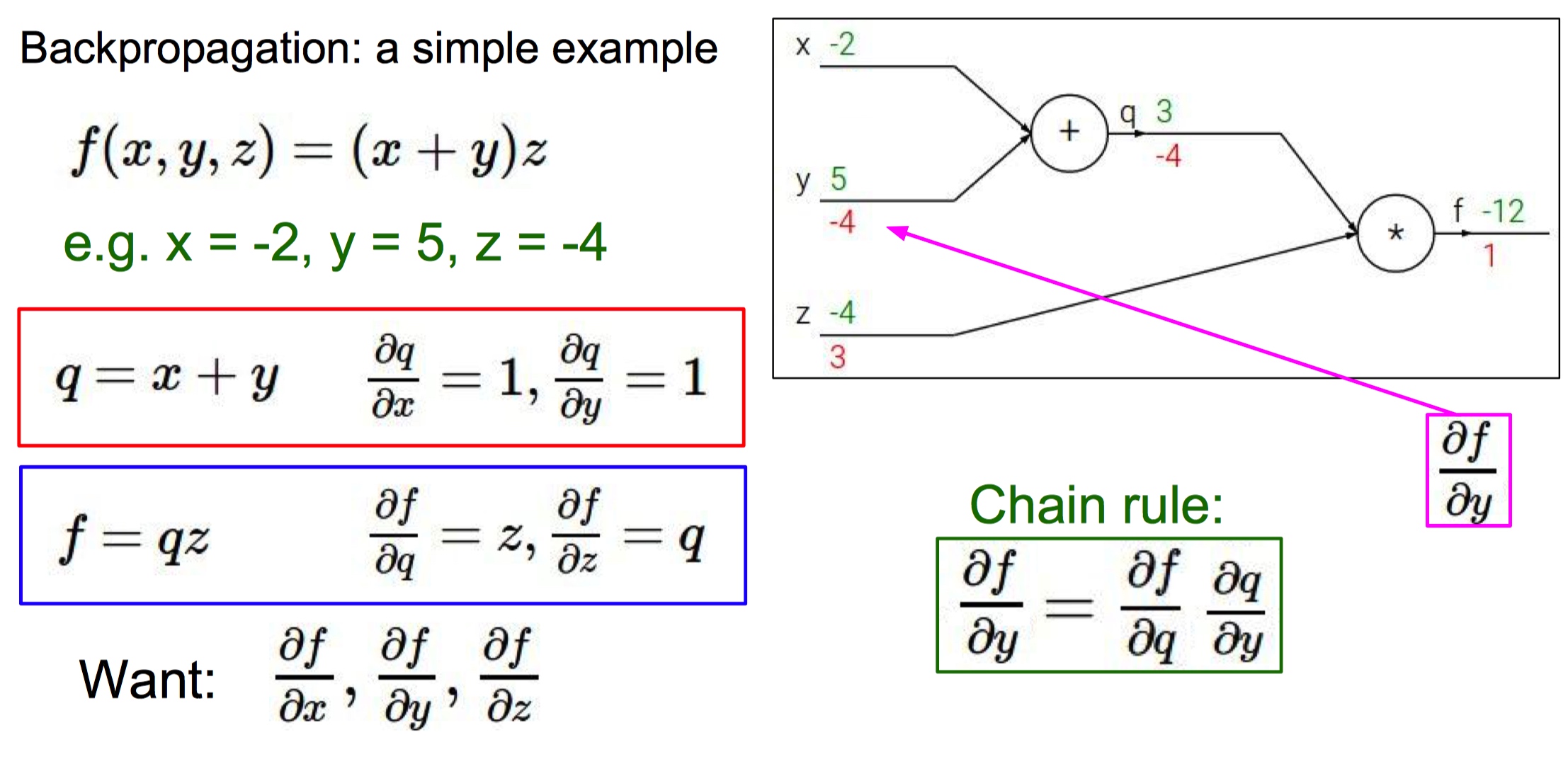
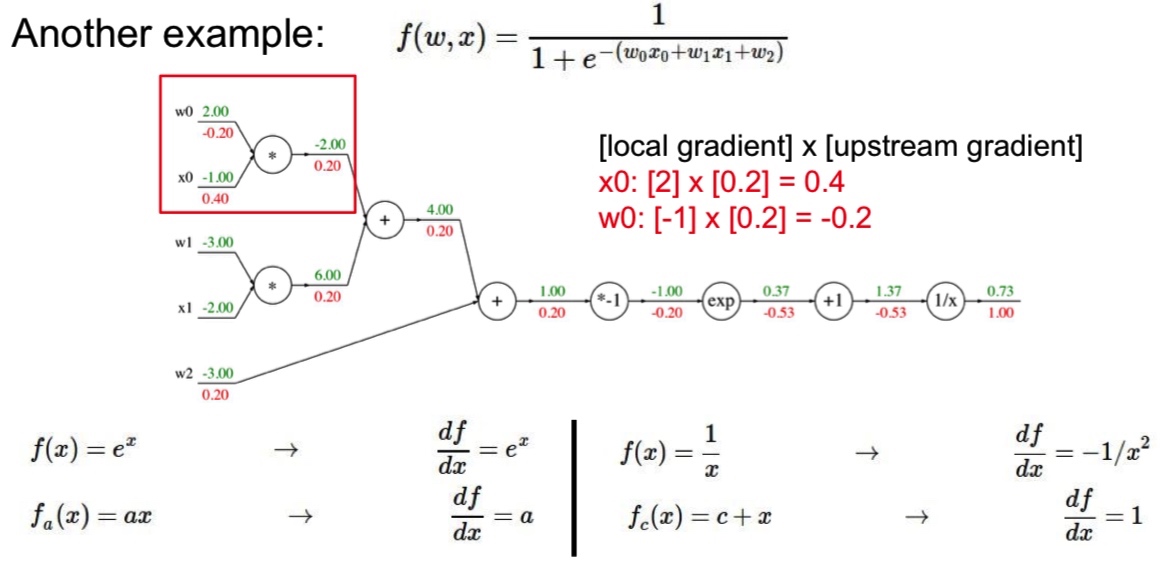
PG 的例子
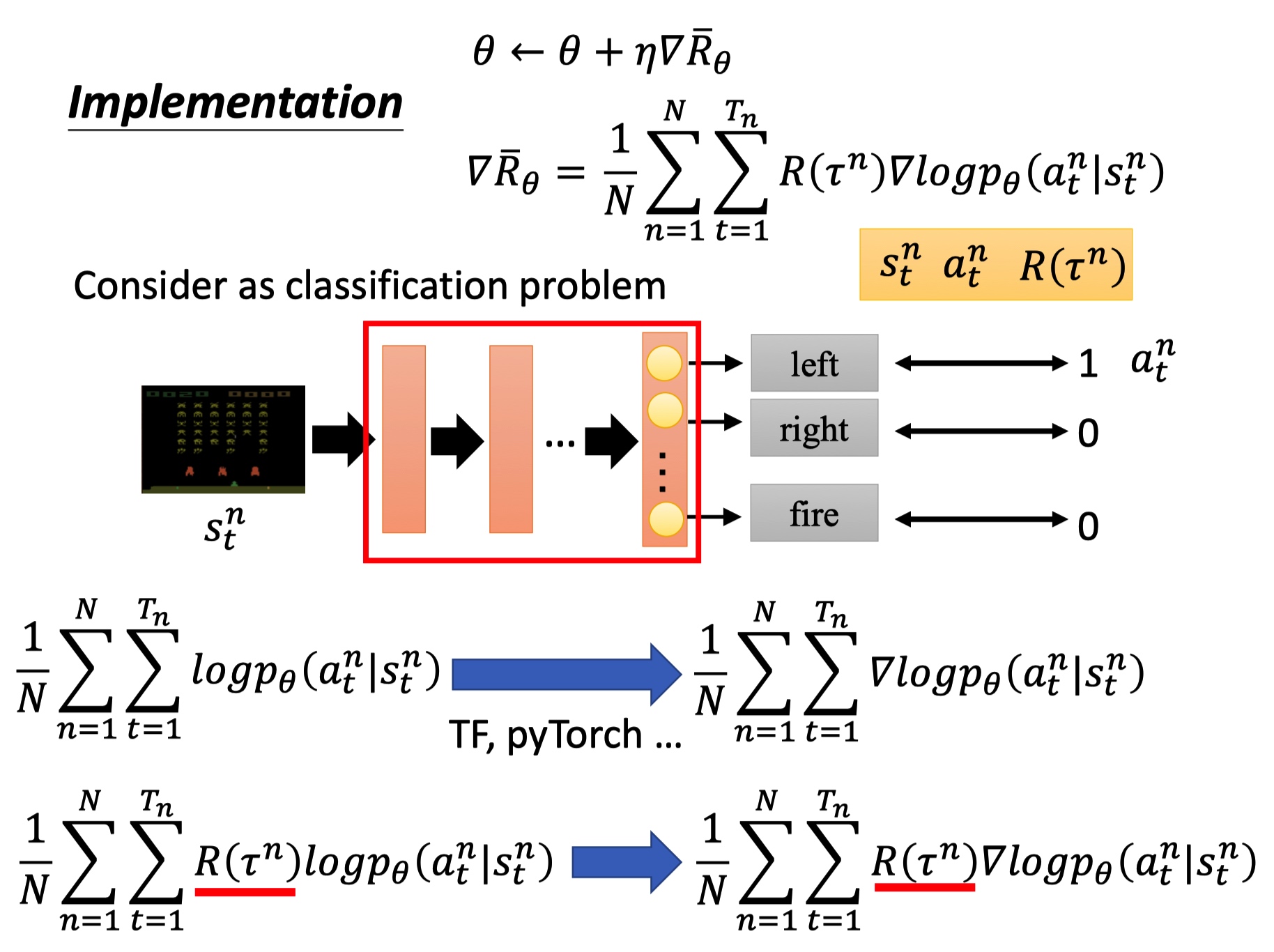
训练 actor 的过程看成是分类任务:输入 state ,输出 action。
最下面公式分别是反向传播梯度计算和 PG 的反向梯度计算,PG 中要乘以整个轨迹的 R。
tip 1: add a baseline
强化学习的优化和样本质量有关,避免采样不充分。Reawrd 函数变成 R-b,代表回报小于 b 的都被我们当成负样本,这样模型能去学习得分更高的动作。b 一般可以使用 R 的均值。
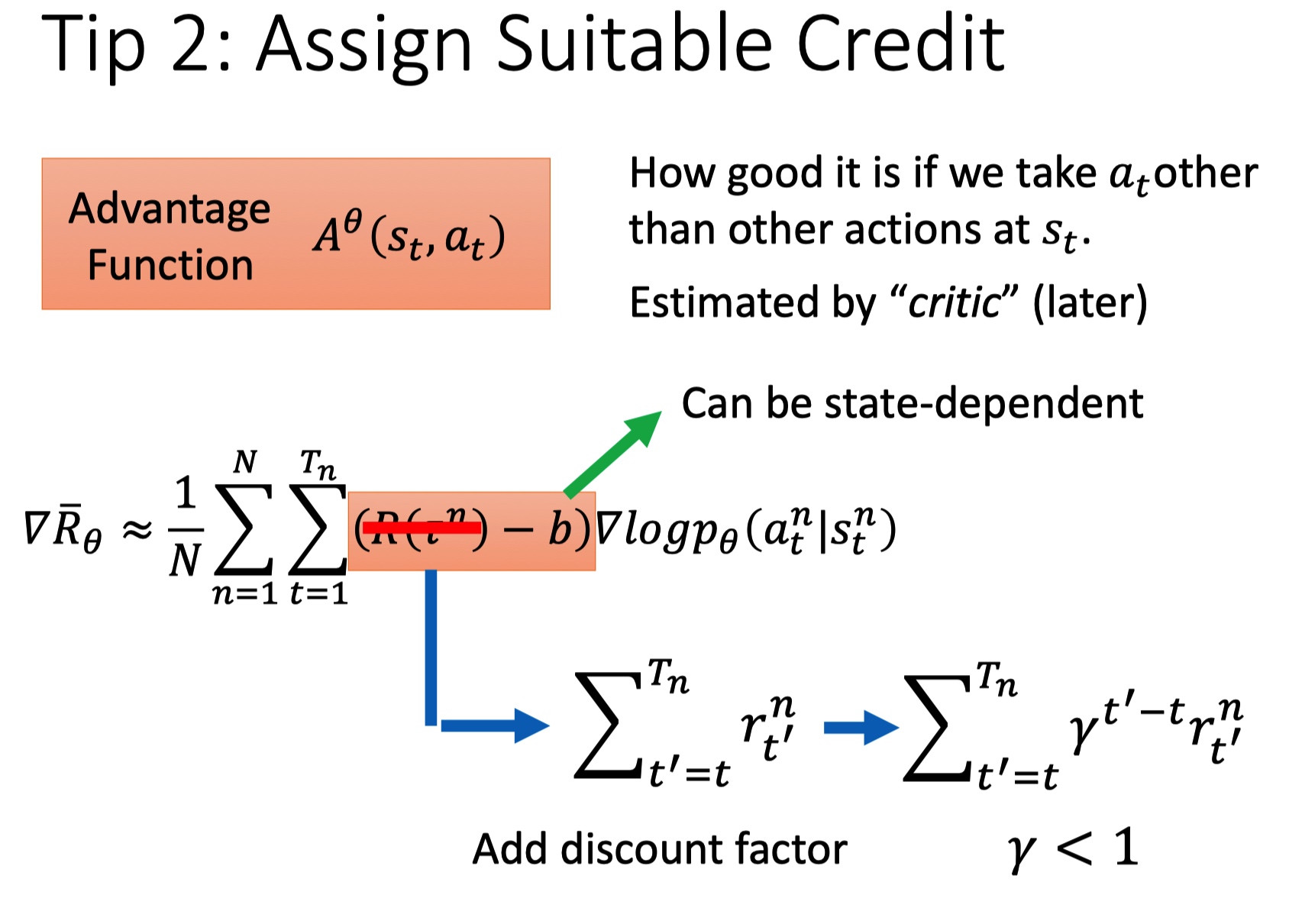
tip 2: assign suitable credit
一场游戏中,不论动作好坏,总会乘上相同的权重 R,这种方法是不合理的,希望每个 action 的权重不同。
- 引入一个 discount rate,对 t 之后的动作 r 进行降权重。
- 利用 Advantage Function 评价状态 s 下动作 a 的好坏 critic。
PPO: Proximal Policy Optimization
importance sampling
假设需要估计期望 Ex p[f(x)],x 符合 p 分布,将期望写成积分的形式。由于在 P 分布下面很难采样,把问题转化到已知 q 分布上,得到在 p 分布下计算期望公式。
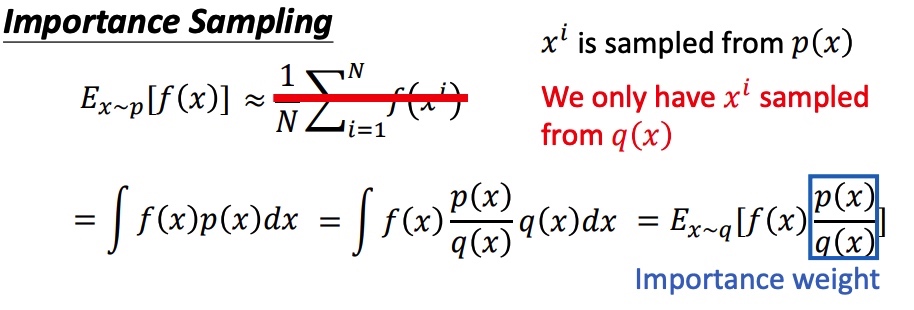
上面方法得到 p 和 q 期望接近,但是方差可能相差很大,且和 q(x)p(x) 有关。
原分布的方差:
Varx−p[f(x)]=Ex−p[f(x)2]−(Ex−q[f(x)])2
新分布的方差:
Varx∼p[f(x)]=Ex∼p[f(x)2]−(Ex∼p[f(x)])2Varx∼q[f(x)q(x)p(x)]=Ex∼q[(f(x)q(x)p(x))2]−(Ex∼q[f(x)q(x)p(x)])2=Ex∼p[f(x)2q(x)p(x)]−(Ex∼p[f(x)])2
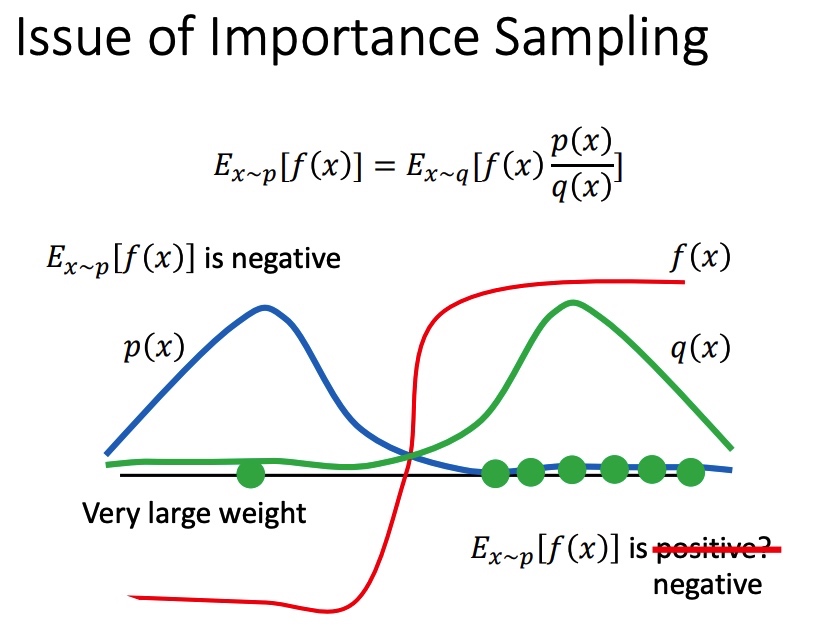
在 p 和 q 分布不一致时,且采样不充分时,可能会带来比较大的误差。
从 On-policy 到 Off-policy
on-policy 时,PG 每次参数更新完成后,actor 就改变了,不能使用之前的数据,必须和环境重新互动收集数据。引入 pθ′ 进行采样,就能将 PG 转为 off-ploicy。

和之前相比,相当于引入重要性采样,所以也有前一节中提到的重要性采样不足问题。
Jθ′(θ)=E(st,at)∼πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)]
PPO/TRPO
为了克服采样的分布与原分布差距过大的不足,PPO 引入 KL 散度进行约束。KL 散度用来衡量两个分布的接近程度。
JPPOθ′(θ)=Jθ′(θ)−βKL(θ,θ′)
TRPO(Trust Region Policy Optimization),要求 KL(θ,θ′)<δ。
JTRPOθ′(θ)=E(st,at)∼πθ′[pθ′(at∣st)pθ(at∣st)Aθ′(st,at)]
KL 散度可能比较难计算,在实际中常使用 PPO2。
- A>0,代表当前策虑表现好。需要增大 π(θ),通过 clip 增加一个上限,防止 π(θ) 和旧分布变化太大。
- A<0,代表当前策虑表现差,不限制新旧分布的差异程度,只需要大幅度改变 π(θ)。
参考 【点滴】策略梯度之PPO - 知乎

PPO algorithm
系数 β 在迭代的过程中需要进行动态调整。引入 KLmaxKLmin,KL > KLmax,说明 penalty 没有发挥作用,增大 β。

Q-Learning
value-base 方法,利用 critic 网络评价 actor 。通过状态价值函数 Vπ(s) 来衡量预期的期望。V 和 pi、s 相关。
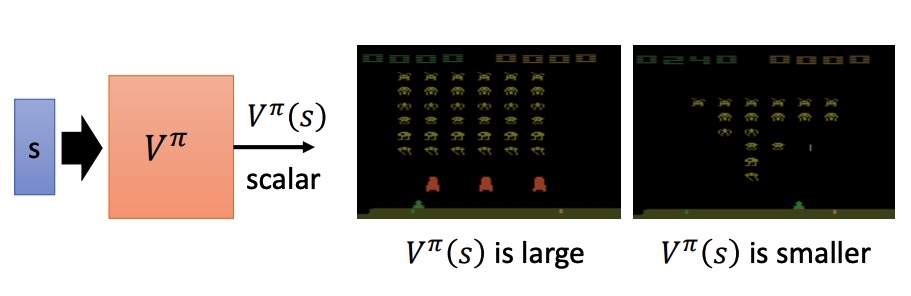
- Monte-Carlo MC: 训练网络使预测的 Vπ(sa) 和实际完整游戏 reward Ga 接近。
- Temporal-difference TD: 训练网络尽量满足 Vπ(st)=Vπ(st+1)+rt 等式,两个状态之间的收益差。
MC: 根据策虑 π 进行游戏得到最后的 G(a),最终存在方差大的问题。Var[kX]=k2Var[X]
TD: r 的方差比较小,Vπ(st+1) 在采样不充分的情况下,可能不准确。

Another Critic
State-action value function Qπ(s,a):预测在 pi 策略下,pair(s, a) 的值。相当于假设 state 情况下强制采取 action a。
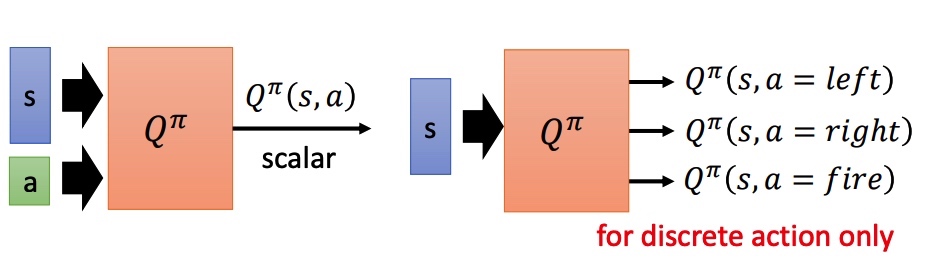
对于非分类的方法:
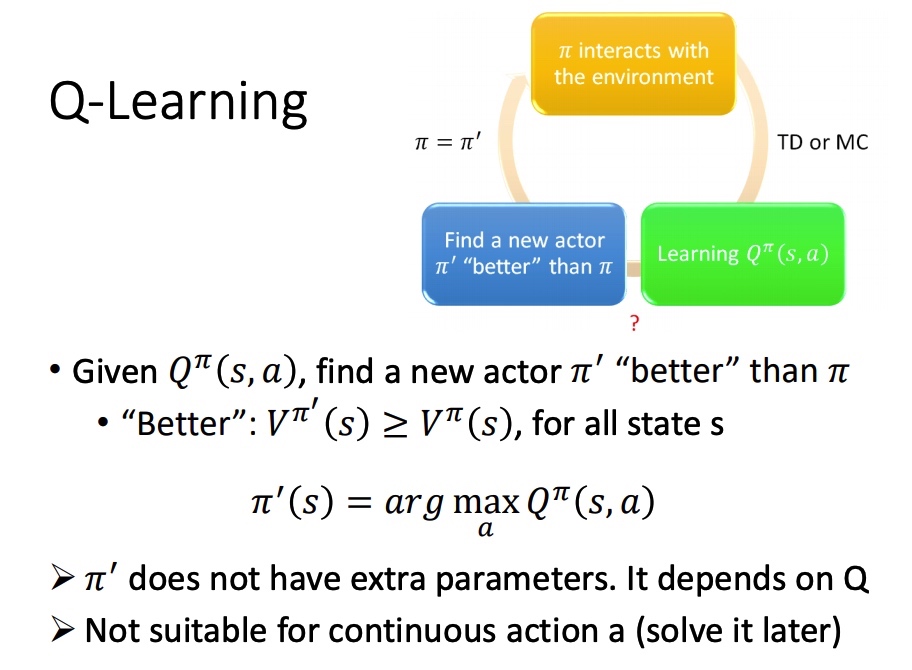
Q-Learning
- 初始 actor π 与环境互动
- 学习该 actor 对应的 Q function
- 找一个比 π 好的策虑:π′,满足 Vπ′(s,a)≥Vπ(s,a), π′(s)=argmaxaQπ(s,a)
在给定 state 下,分别代入 action,取函数值最大的 a,作为后面对该 state 时采取的 action。
证明新的策虑存在:

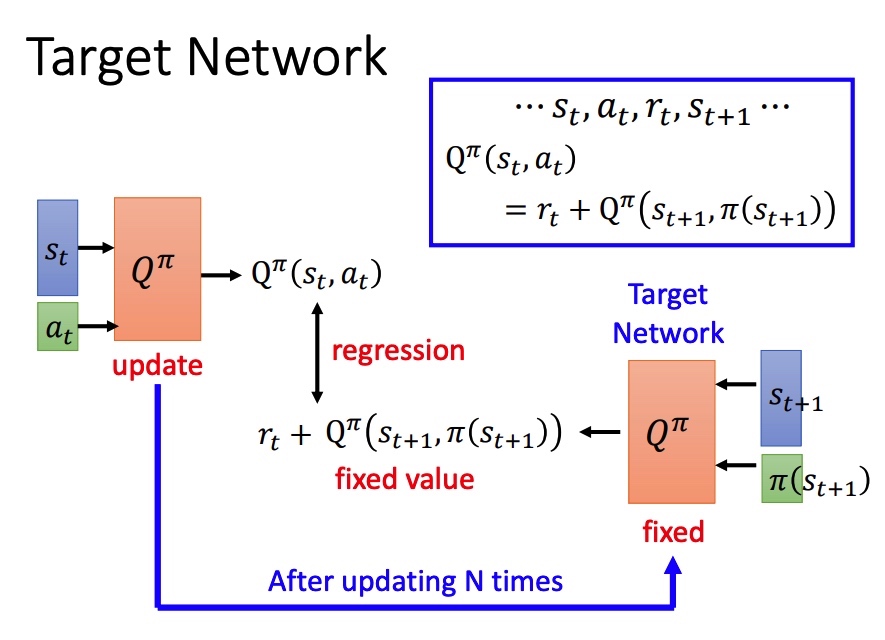
Target NetWork
左右两边的网络相同,如果同时训练比较困难。简单的想法是固定右边的网络进行训练,一定次数后再拷贝左边的网络。
Exploration
Q function 导致 actor 每次都会选择具有更大值的 action,无法准确估计某一些动作,对于收集数据而言是一个弊端。
- Epsilon Greedy
- Boltzmann Exploration
- 利用 softmax 计算选取动作的概率,然后进行采样

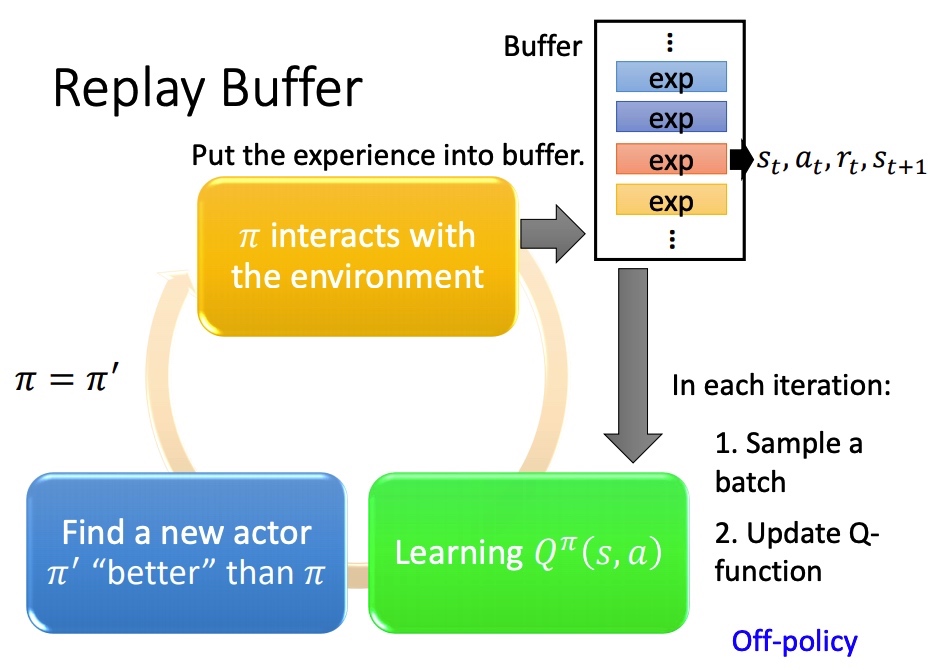
Replay buffer
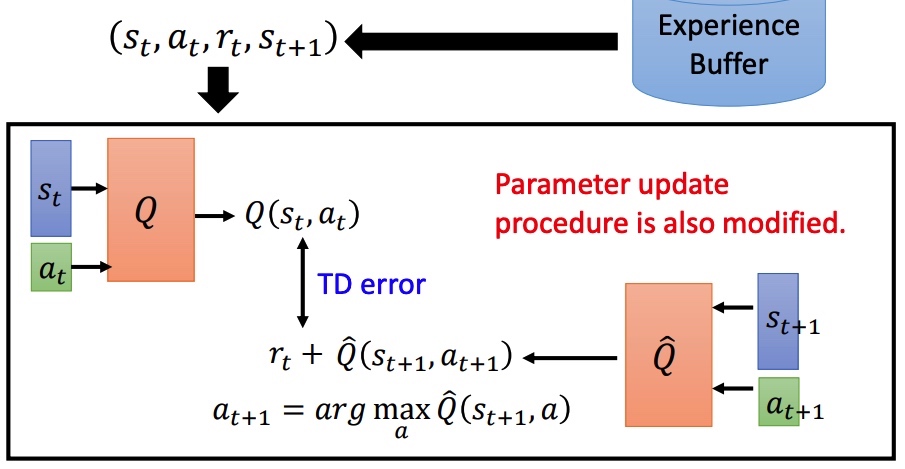
采样之后的 (st,at,rt,st+1) 保存在一个 buffer 里面(可能是不同策虑下采样得到的),每次训练从 buffer 中 sample 一个 batch。
结果:训练方法变成 off-policy。减少 RL 重复采样,充分利用数据。
Typical Q-Learning Algorithm
Q-Learning 流程:

Double DQN DDQN
- Q value 容易高估:目标值 rt+maxQ(st+1,a) 倾向于选择被高估的 action,导致 target 很大。
- 选动作的 Q’ 和计算 value 的 Q(target network) 不同。Q 中高估 a,Q’ 可能会准确估计 V 值。Q’ 中高估 a ,可能不会被 Q 选中。

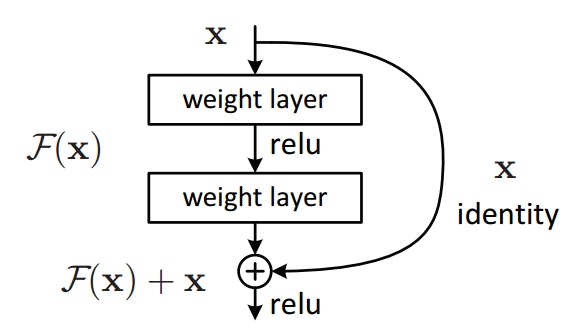
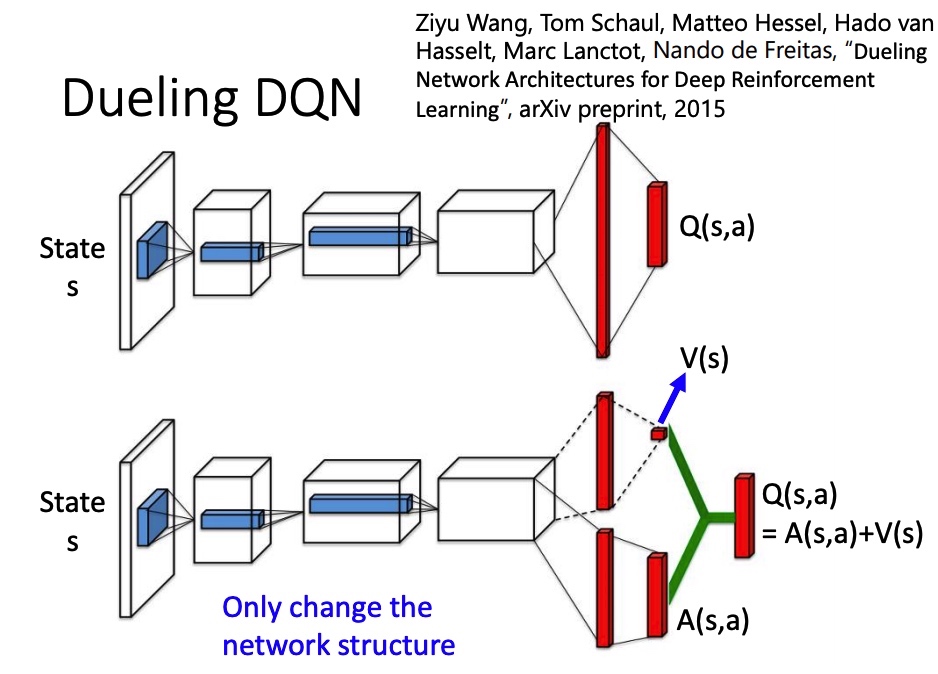
Dueling DQN
改 network 架构。V(s) 代表 s 所具有的价值,不同的 action 共享。 A(s,a) advantage function 代表在 s 下执行 a 的价值。最后 Q(s,a)=A(s,a)+V(s)。
为了让网络倾向于使用 V(能训练这个网络),得到 A 后,要对 A 做 normalize。
Prioritized Reply
在训练过程中,对于经验 buffer 里面的样本,TD error 比较大的样本有更大的概率被采样,即难训练的数据增大被采样的概率。
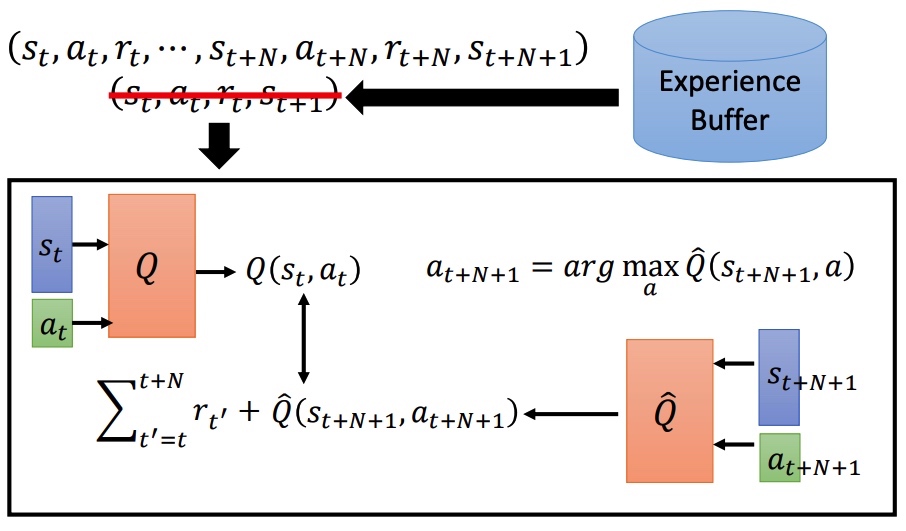
Multi-step
综合 MC 和 TD 的优点,训练样本按一定步长 N 进行采样。MC 准确方差大,TD 方差小,估计不准。
Noisy Net

- Noise on Action:在相同状态下,可能会采取不同的动作。
- Noise on Parameters:开始时加入噪声。同一个 episode 内,参数不会改变。相同状态下,动作相同。
更好探索环境。
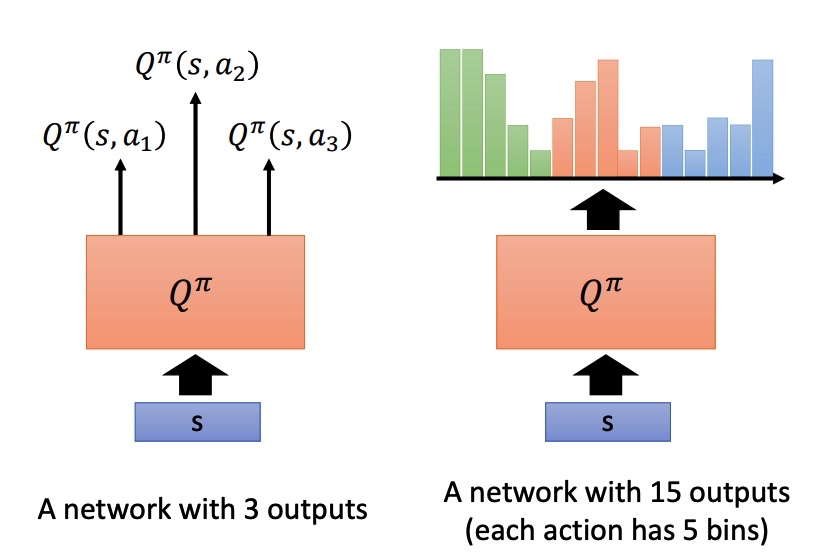
Distributional Q-function
Q 是累积收益的期望,实际上在 s 采取 a 时,最终所有得到的 reward 为一个分布 reward distribution。部分时候分布不同,可能期望相同,所以用期望来代替 reward 会损失一些信息。
Distributional Q-function 直接输出分布,均值相同时,采取方差小的方案。这种方法不会产生高估 q 值的情况。
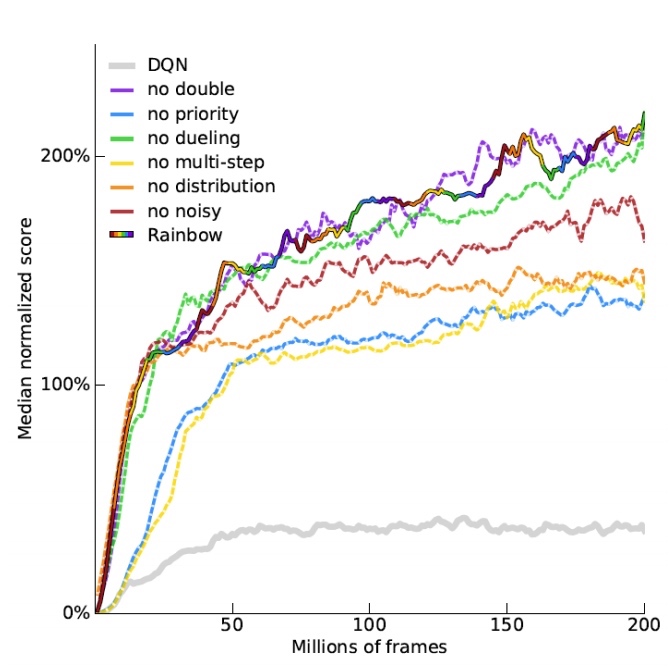
Rainbow
rainbow 是各种策略的混合体。
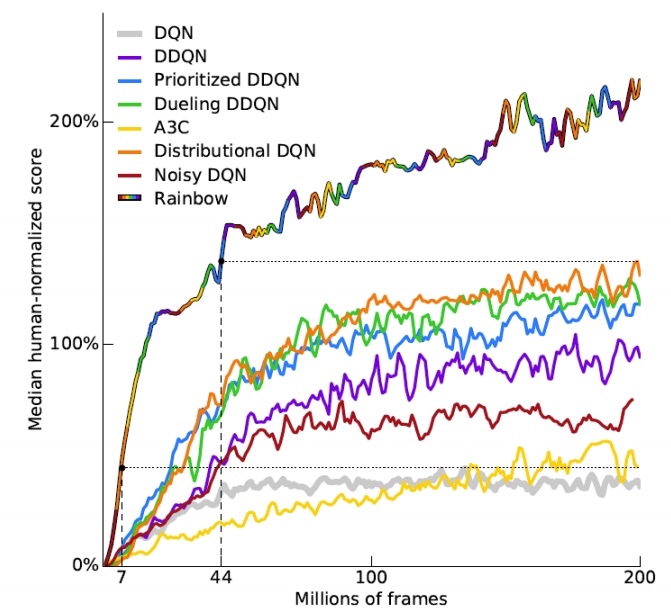
DDQN 影响不大。
Continuous Actions
action 是一个连续的向量,Q-learning 不是一个很好的方法。
a=argamaxQ(s,a)
- 从 a 中采样出一批动作,看哪个行动 Q 值最大。
- 使用 gradient ascent 解决最优化问题。
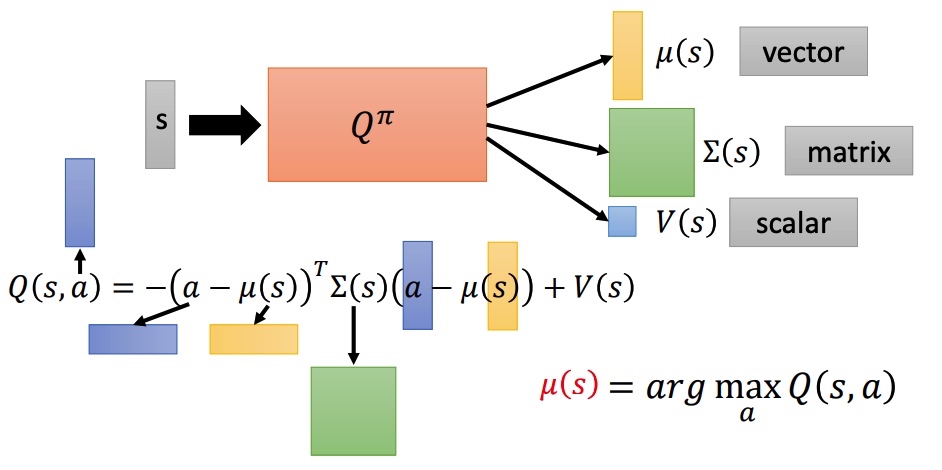
- 设计一个网络来化简过程。
- ∑ 和 μ 是高斯分布的方差和均值,保证矩阵一定是正定。
- 最小化下面的函数,需要最小化 a−μ。
Reference